题目内容
两个都以O为圆心的同心圆,大圆的半径为3,小圆的半径为0.8,在大圆上取三点A、B、C,使∠ACB=30°,试判断小圆与直线AB的位置关系,并给予证明.
考点:直线与圆的位置关系
专题:常规题型
分析:如图,连接OA、OB,作OD⊥AB于D,根据圆周角定理得到∠AOB=2∠ACB=60°,则可判断△OAB为等边三角形,根据等边三角形的性质得OD=
OA=
,
而小圆的半径为0.8,于是根据直线与圆的位置关系可判断小圆与直线AB的位置关系是相离.
| ||
| 2 |
3
| ||
| 2 |
而小圆的半径为0.8,于是根据直线与圆的位置关系可判断小圆与直线AB的位置关系是相离.
解答:解:小圆与直线AB相离.理由如下:
如图, 连接OA、OB,作OD⊥AB于D,
连接OA、OB,作OD⊥AB于D,
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
而OA=OB,
∴△OAB为等边三角形,
∵OD⊥AB,
∴OD=
OA=
,
而小圆的半径为0.8,
∴圆心O到AB的距离大于小圆的半径,
∴小圆与直线AB的位置关系是相离.
如图,
 连接OA、OB,作OD⊥AB于D,
连接OA、OB,作OD⊥AB于D,∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
而OA=OB,
∴△OAB为等边三角形,
∵OD⊥AB,
∴OD=
| ||
| 2 |
3
| ||
| 2 |
而小圆的半径为0.8,
∴圆心O到AB的距离大于小圆的半径,
∴小圆与直线AB的位置关系是相离.
点评:本提考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目

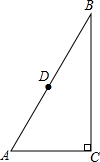 如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,3cm为半径作圆.试判断:
如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,3cm为半径作圆.试判断: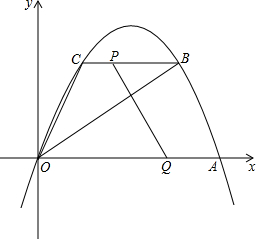 抛物线经过原点O(0,0),A(20,0),C(4,8),过C作平行于x轴的直线与抛物线另一交点为B,连OC,OB.
抛物线经过原点O(0,0),A(20,0),C(4,8),过C作平行于x轴的直线与抛物线另一交点为B,连OC,OB.