题目内容
在以点O为圆心的两个同心圆中，大圆的弦CD交小圆于E、F，OE、OF的延长线交大圆于点A、B，试说明
=
．
 |
| AC |
|
| BD |
考点：圆心角、弧、弦的关系
专题：证明题
分析：连接OC、OD，则△OCD和△OEF都是等腰三角形，有∠OCD=∠ODC，∠OEF=∠OFE，由三角形的外角等于与它不相邻的两个内角和，得∠AOC=∠BOD，再由在同圆中相等的圆心角对的弧相等得
=
．
|
| AC |
|
| BD |
解答：
证明：连接OC、OD，
∵OC=OD，OE=OF，
∴∠OCD=∠ODC，∠OEF=∠OFE，
∵∠OEF=∠OCD+∠AOC，∠OFE=∠ODC+∠BOD，
∴∠AOC=∠BOD，
∴
=
．
证明：连接OC、OD，∵OC=OD，OE=OF，
∴∠OCD=∠ODC，∠OEF=∠OFE，
∵∠OEF=∠OCD+∠AOC，∠OFE=∠ODC+∠BOD，
∴∠AOC=∠BOD，
∴
|
| AC |
|
| BD |
点评：本题考查的是圆心角、弧、弦的关系定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等．准确作出辅助线是解答此题的关键．
练习册系列答案
相关题目
小敏按照一定规律写了四个数：
，1，
，
，按此规律第5个数应该是（ ）
| 2 |
| 3 |
| 3 |
| 2 |
| 9 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，在四边形ABCD中，AB∥CD，∠D=90°，以D为圆心，AD为半经的⊙D与直线BC相切于点E．求证：BC=CD．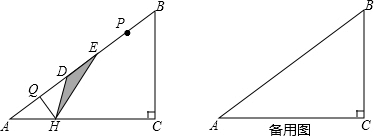
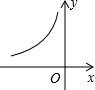如图是反比例函数y=