题目内容
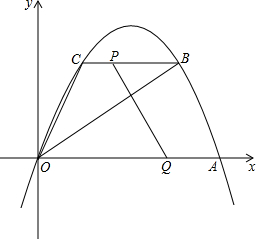 抛物线经过原点O(0,0),A(20,0),C(4,8),过C作平行于x轴的直线与抛物线另一交点为B,连OC,OB.
抛物线经过原点O(0,0),A(20,0),C(4,8),过C作平行于x轴的直线与抛物线另一交点为B,连OC,OB.(1)求抛物线解析式;
(2)点P由C以每秒2个单位的速度向B运动,同时点Q由A以每秒4个单位的速度向O运动,联结PQ,设运动时间为t秒:
①当PQ=OC时,求t的值;
②当PQ⊥OB时,写出t的值.
考点:二次函数综合题
专题:
分析:(1)直接利用待定系数法求二次函数解析式得出即可;
(2)①利用已知表示出CO以及PQ的长,结合勾股定理求出即可;
②利用四边形面积结合三角形面积公式得出等式
×
×8
=128-24t,进而求出即可.
(2)①利用已知表示出CO以及PQ的长,结合勾股定理求出即可;
②利用四边形面积结合三角形面积公式得出等式
| 1 |
| 2 |
| (16-6t)2+82 |
| 5 |
解答: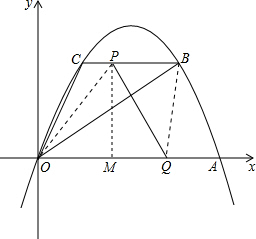 解:(1)∵抛物线经过原点O(0,0),A(20,0),
解:(1)∵抛物线经过原点O(0,0),A(20,0),
∴设抛物线解析式为:y=ax(x-20)(a≠0),
∵抛物线过点C(4,8),
∴8=4a×(4-20),
解得:a=-
,
故抛物线解析式为:y=-
x2+
x;
(2)①过点P作PM⊥OA于点M,
设t秒后,可得P(4+2t,8),Q(20-4t,0),
则PM=8,QM=20-4t-(4+2t)=16-6t
若PQ=OC,
则(16-6t)2+82=42+82,
解得:t1=
,t2=2,
②连接OP,BQ,
当y=8,则8=-
x2+
x,
解得:x1=4,x2=16,
故B(16,8),则BO=8
,
∵PQ⊥OB,
∴S四边形OPBQ=
×BO×PQ=
×
×8
,
∵
×PB×8+
×QO×8=
(16-4-2t)×8+
×(20-4t)×8
=128-24t,
故
×
×8
=128-24t,
则80[(16-6t)2+64]=(128-24t)2,
整理得:t2-4t+4=0,
解得:t1=t2=2,
故当PQ⊥OB时,t=2.
 解:(1)∵抛物线经过原点O(0,0),A(20,0),
解:(1)∵抛物线经过原点O(0,0),A(20,0),∴设抛物线解析式为:y=ax(x-20)(a≠0),
∵抛物线过点C(4,8),
∴8=4a×(4-20),
解得:a=-
| 1 |
| 8 |
故抛物线解析式为:y=-
| 1 |
| 8 |
| 5 |
| 2 |
(2)①过点P作PM⊥OA于点M,
设t秒后,可得P(4+2t,8),Q(20-4t,0),
则PM=8,QM=20-4t-(4+2t)=16-6t
若PQ=OC,
则(16-6t)2+82=42+82,
解得:t1=
| 10 |
| 3 |
②连接OP,BQ,
当y=8,则8=-
| 1 |
| 8 |
| 5 |
| 2 |
解得:x1=4,x2=16,
故B(16,8),则BO=8
| 5 |
∵PQ⊥OB,
∴S四边形OPBQ=
| 1 |
| 2 |
| 1 |
| 2 |
| (16-6t)2+82 |
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=128-24t,
故
| 1 |
| 2 |
| (16-6t)2+82 |
| 5 |
则80[(16-6t)2+64]=(128-24t)2,
整理得:t2-4t+4=0,
解得:t1=t2=2,
故当PQ⊥OB时,t=2.
点评:此题主要考查了二次函数综合以及勾股定理和四边形面积公式等知识,熟练应用勾股定理是解题关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
小敏按照一定规律写了四个数:
,1,
,
,按此规律第5个数应该是( )
| 2 |
| 3 |
| 3 |
| 2 |
| 9 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
对于四条线段a、b、c、d,如果ab=cd,那么( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
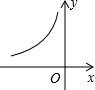 如图是反比例函数y=
如图是反比例函数y=