题目内容
已知△ABC中,有两个内角分别为45°和60°,若一边长为4,求该△ABC的面积.
考点:解直角三角形
专题:分类讨论
分析:需要分类讨论:边长为4的边所对的内角不同.通过作高线AD将△ABC化为两个直角三角形,通过解这2个直角三角形求得BC、AD的长度,然后由三角形的面积公式进行解答.
解答: 解:如图,过点A作AD⊥BC于点D.
解:如图,过点A作AD⊥BC于点D.
①当AB=4时.
在Rt△ABD中,AD=BD=AB•sin45°=2
.
在Rt△ACD中,CD=AD•cot60°=
.
则BC=BD+CD=2
+
.
所以 S△ABC=
BC•AD=
×(2
+
)×2
=4+
;
②当BC=4时,设AD=x,则BD=AD=x,CD=4-x.
在Rt△ACD中,CD=AD•cot60°,即4-x=
x,
解得 x=6-2
,
故 S△ABC=
BC•AD=
×4×(6-2
)=12-4
;
③当AC=4时.
在Rt△ACD中,CD=AC•cos60°=4×
=2,AD=AC•sin60°=4×
=2
.
则BD=AD=2
,
则S△ABC=
BC•AD=
×(2
+2)×2
=6+2
.
 解:如图,过点A作AD⊥BC于点D.
解:如图,过点A作AD⊥BC于点D.①当AB=4时.
在Rt△ABD中,AD=BD=AB•sin45°=2
| 2 |
在Rt△ACD中,CD=AD•cot60°=
| 2 |
| 3 |
| 6 |
则BC=BD+CD=2
| 2 |
| 2 |
| 3 |
| 6 |
所以 S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 6 |
| 2 |
4
| ||
| 3 |
②当BC=4时,设AD=x,则BD=AD=x,CD=4-x.
在Rt△ACD中,CD=AD•cot60°,即4-x=
| ||
| 3 |
解得 x=6-2
| 3 |
故 S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
③当AC=4时.
在Rt△ACD中,CD=AC•cos60°=4×
| 1 |
| 2 |
| ||
| 2 |
| 3 |
则BD=AD=2
| 3 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
点评:本题考查了解直角三角形.本题中没有指明4是那一条边的长度,所以需要对该边进行分类讨论,以防漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
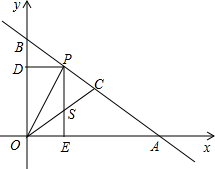 如图,一次函数y=-
如图,一次函数y=-
 如图,∠CAB=90°,AC=2,∠B=30°,作AC1⊥BC,再过点C1作C1A1⊥AB,…求图中所有阴影部分的面积.
如图,∠CAB=90°,AC=2,∠B=30°,作AC1⊥BC,再过点C1作C1A1⊥AB,…求图中所有阴影部分的面积.