题目内容
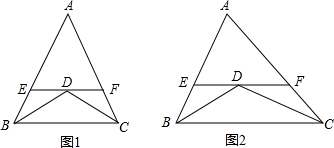
(1)如图1,在△ABC中,AB=AC,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于点E、F,则EF与BE、CF之间有何数量关系?请说明理由;
(2)如图2,将(1)中的“在△ABC中,AB=AC“改为“若△ABC不是等腰三角形“,其他条件不变,那么(1)中的结论是否仍然成立?写出结论,不必说明理由.
(2)如图2,将(1)中的“在△ABC中,AB=AC“改为“若△ABC不是等腰三角形“,其他条件不变,那么(1)中的结论是否仍然成立?写出结论,不必说明理由.

考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)根据角平分线的定义可得∠EBD=∠CBD,∠FCD=∠BCD,再根据两直线平行,内错角相等可得∠EDB=∠CBD,∠FDC=∠BCD,然后求出∠EBD=∠EDB,∠FDC=∠BCD,再根据等角对等边可得BE=DE,CF=DF,然后解答即可.
(2)根据角平分线的定义可得∠EBD=∠CBD,∠FCD=∠BCD,再根据两直线平行,内错角相等可得∠EDB=∠CBD,∠FDC=∠BCD,然后求出∠EBD=∠EDB,∠FDC=∠BCD,再根据等角对等边可得BE=DE,CF=DF,然后解答即可.
(2)根据角平分线的定义可得∠EBD=∠CBD,∠FCD=∠BCD,再根据两直线平行,内错角相等可得∠EDB=∠CBD,∠FDC=∠BCD,然后求出∠EBD=∠EDB,∠FDC=∠BCD,再根据等角对等边可得BE=DE,CF=DF,然后解答即可.
解答:解:(1)BE+CF=EF.理由如下:
如图1,∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,
∴BE=DE,CF=DF,
∴BE+CF=DE+DF=EF,
即BE+CF=EF.
(2)BE+CF=EF仍然成立,理由如下:
如图2,∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,
∴BE=DE,CF=DF,
∴BE+CF=DE+DF=EF,
即BE+CF=EF.
如图1,∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,
∴BE=DE,CF=DF,
∴BE+CF=DE+DF=EF,
即BE+CF=EF.
(2)BE+CF=EF仍然成立,理由如下:
如图2,∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD,
∵EF∥BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠BCD,
∴BE=DE,CF=DF,
∴BE+CF=DE+DF=EF,
即BE+CF=EF.
点评:本题考查了等腰三角形的判定与性质,平行线的性质,主要利用了角平分线的定义,两直线平行,内错角相等的性质,等角对等边的性质.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
八年级某班50名学生的年龄统计结果如表所示,则此班学生年龄数据的众数、中位数分别为( )
| 年龄 | 13 | 14 | 15 | 16 |
| 人数 | 6 | 20 | 21 | 3 |
| A、14,14 |
| B、15,14 |
| C、14,15 |
| D、15,16 |
 如图,正方形ABCD对角线AC、BD交于O,DE平分∠ADB,CN⊥DE于N,求证:OF=
如图,正方形ABCD对角线AC、BD交于O,DE平分∠ADB,CN⊥DE于N,求证:OF=