题目内容
已知关于x的一元二次方程(m-1)x2-(2m+3)x+(m+3)=0有两个实数根.
(1)求m的取值范围;
(2)请写出取值范围内最小的负整数m.并求出此时方程的两个根.
(1)求m的取值范围;
(2)请写出取值范围内最小的负整数m.并求出此时方程的两个根.
考点:根的判别式,一元二次方程的定义
专题:
分析:(1)根据一元二次方程的定义和判别式的意义得到m-1≠0且△=[-(2m+3)]2-4(m-1)(m+3)≥0,然后解不等式即可;
(2)根据(1)的结论得到m满足条件的最小负整数为-3,则原方程化为-4x2+3x=0,然后利用因式分解法解方程.
(2)根据(1)的结论得到m满足条件的最小负整数为-3,则原方程化为-4x2+3x=0,然后利用因式分解法解方程.
解答:解:(1)根据题意得m-1≠0且△=[-(2m+3)]2-4(m-1)(m+3)≥0,
解得m≥-3且m≠1;
(2)m满足条件的最小负整数为-3,则原方程化为-4x2+3x=0,
∴-x(4x-3)=0,
∴x1=0,x2=
.
解得m≥-3且m≠1;
(2)m满足条件的最小负整数为-3,则原方程化为-4x2+3x=0,
∴-x(4x-3)=0,
∴x1=0,x2=
| 3 |
| 4 |
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义.

练习册系列答案
相关题目
 如图,正方形ABCD对角线AC、BD交于O,DE平分∠ADB,CN⊥DE于N,求证:OF=
如图,正方形ABCD对角线AC、BD交于O,DE平分∠ADB,CN⊥DE于N,求证:OF=
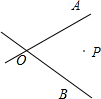 如图,两条公路OA、OB相交,在两条公路中间有一个油库,设为点P,如在两条公路上各设置一个加油站,请你设置一个方案,把两个加油站设在何处,可使油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短.
如图,两条公路OA、OB相交,在两条公路中间有一个油库,设为点P,如在两条公路上各设置一个加油站,请你设置一个方案,把两个加油站设在何处,可使油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短.