题目内容
 如图,∠CAB=90°,AC=2,∠B=30°,作AC1⊥BC,再过点C1作C1A1⊥AB,…求图中所有阴影部分的面积.
如图,∠CAB=90°,AC=2,∠B=30°,作AC1⊥BC,再过点C1作C1A1⊥AB,…求图中所有阴影部分的面积.考点:勾股定理,含30度角的直角三角形
专题:规律型
分析:用面积法求出AC1,再根据三角函数求出A1C1,A1C2,A3C3…,AA1,A1A2,A2A3…,从而表示出△AA1C1的面积,△A1A2C2的面积,△A1A2C2的面积,发现为无穷等比数列,用极限求解即可.
解答:解:∵AC=2,∠B=30°,
∴BC=4,
∴AB=2
,
∴BC•AC1=AC•AB,
∴4AC1=2×2
,
∴AC1=
,
则A1C1=
cos30°=
,
A1C2=A1C1cos30°=
,
同理可得,A2C2=
,
A2C3=
,
A3C3=
,
…
AA1=
×tan30°=
,
A1A2=
×tan30°=
,
A2A3=
×tan30°=
,
…
△AA1C1的面积为
AA1•A1C1=
×
×
=
,
△A1A2C2的面积为
A1A2•A2C2=
×
×
=
,
△A1A2C2的面积为
A1A3•A3C3=
×
×
=
,
S阴影=
+
+
+…=
=
.
∴BC=4,
∴AB=2
| 3 |
∴BC•AC1=AC•AB,
∴4AC1=2×2
| 3 |
∴AC1=
| 3 |
则A1C1=
| 3 |
| 3 |
| 2 |
A1C2=A1C1cos30°=
3
| ||
| 4 |
同理可得,A2C2=
| 9 |
| 8 |
A2C3=
9
| ||
| 16 |
A3C3=
| 27 |
| 32 |
…
AA1=
| 3 |
| 2 |
| ||
| 2 |
A1A2=
| 9 |
| 8 |
3
| ||
| 8 |
A2A3=
| 27 |
| 32 |
9
| ||
| 32 |
…
△AA1C1的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
3
| ||
| 8 |
△A1A2C2的面积为
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 8 |
| 9 |
| 8 |
27
| ||
| 128 |
△A1A2C2的面积为
| 1 |
| 2 |
| 1 |
| 2 |
9
| ||
| 32 |
| 27 |
| 32 |
243
| ||
| 2048 |
S阴影=
3
| ||
| 8 |
27
| ||
| 128 |
243
| ||
| 2048 |
| lim |
| n→∞ |
| ||||||
1-
|
6
| ||
| 7 |
点评:本题考查了含30°角的直角三角形,涉及三角形的面积、等比数列、极限等知识,重在探究规律.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
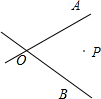 如图,两条公路OA、OB相交,在两条公路中间有一个油库,设为点P,如在两条公路上各设置一个加油站,请你设置一个方案,把两个加油站设在何处,可使油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短.
如图,两条公路OA、OB相交,在两条公路中间有一个油库,设为点P,如在两条公路上各设置一个加油站,请你设置一个方案,把两个加油站设在何处,可使油车从油库出发,经过一个加油站,再到另一个加油站,最后回到油库所走的路程最短.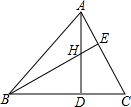 如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.
如图,在△ABC中,高AD、BE交于H点,若BH=AC,求∠ABC的度数.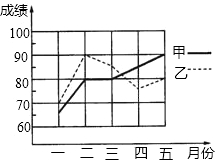 为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.
为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛,统计了他们从今年1到5月的每个月的一次测验成绩(单位:分),如图是两人赛前5次测验成绩的折线统计图.