题目内容
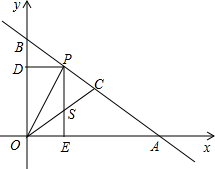 如图,一次函数y=-
如图,一次函数y=-| 3 |
| 4 |
| 3 |
| 2 |
(1)求线段OC所在直线的解析式;
(2)求S与m的函数解析式;
(3)当0<m<4时,求S的最大值;
(4)当S=0.65时,m的值有
考点:一次函数综合题
专题:
分析:(1)在一次函数解析式中令y=
,即可求得C的横坐标,然后利用待定系数法即可求得函数的解析式;
(2)分0≤m≤2和2<m<4两种情况进行讨论,利用三角形的面积公式求解;
(3)分0≤m≤2和2<m<4两种情况,分别利用函数的性质求解;
(4)分0≤m≤2和2<m<4两种情况,分别求得S的范围即可求解.
| 3 |
| 2 |
(2)分0≤m≤2和2<m<4两种情况进行讨论,利用三角形的面积公式求解;
(3)分0≤m≤2和2<m<4两种情况,分别利用函数的性质求解;
(4)分0≤m≤2和2<m<4两种情况,分别求得S的范围即可求解.
解答: 解:(1)在y=-
解:(1)在y=-
x+3中,令y=
,则-
x+3=
,
解得:x=2,
则C的坐标是(2,
),
设OC的解析式是y=kx,则2k=
,
解得:k=
,
则OC的解析式是:y=
x;
(2)P的横坐标是m,则纵坐标是-
m+3,
在y=
x中,令x=m,则y=
m,即S的坐标是(m,
m).
当0≤m≤2时,重合部分是△OPS,则S=
【(-
m+3)-
m】m=-
m2+
m;
当2<m<4时,在y=
x中,令y=-
m+3,则
x=-
m+3,解得:x=-m+4,即F的横坐标是-m+4,则PF=m-(-m+4)=2m-4,
则S=
(2m-4)•(-
m+3),即S=-
m2+
m-6;
(3)0≤m≤2时,则m=1时,S的最大值是:-
+
=
;
当2<m<4时,当m=3时,S的最大值是:-
+
-6=
.
总之,当0<m<4时,S的最大值是
;
(4)当0≤m≤2时,则0<S≤
,则当S=0.65的m的值有2个;
2<m<4时,0<S≤
,则S=0.65的m的值有2个.
故当S=0.65时,m的值有4个.
故答案是:4.
 解:(1)在y=-
解:(1)在y=-| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
解得:x=2,
则C的坐标是(2,
| 3 |
| 2 |
设OC的解析式是y=kx,则2k=
| 3 |
| 2 |
解得:k=
| 3 |
| 4 |
则OC的解析式是:y=
| 3 |
| 4 |
(2)P的横坐标是m,则纵坐标是-
| 3 |
| 4 |
在y=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
当0≤m≤2时,重合部分是△OPS,则S=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
当2<m<4时,在y=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
则S=
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 9 |
| 2 |
(3)0≤m≤2时,则m=1时,S的最大值是:-
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
当2<m<4时,当m=3时,S的最大值是:-
| 27 |
| 4 |
| 27 |
| 2 |
| 3 |
| 4 |
总之,当0<m<4时,S的最大值是
| 3 |
| 4 |
(4)当0≤m≤2时,则0<S≤
| 3 |
| 4 |
2<m<4时,0<S≤
| 3 |
| 4 |
故当S=0.65时,m的值有4个.
故答案是:4.
点评:本题考查了待定系数法求函数的解析式,以及二次函数的性质,正确求得函数的解析式是关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
八年级某班50名学生的年龄统计结果如表所示,则此班学生年龄数据的众数、中位数分别为( )
| 年龄 | 13 | 14 | 15 | 16 |
| 人数 | 6 | 20 | 21 | 3 |
| A、14,14 |
| B、15,14 |
| C、14,15 |
| D、15,16 |