题目内容
已知
+
=1，a2-b2=4，求a和b．
| 4 |
| a2 |
| 9 |
| b2 |
考点：高次方程
专题：
分析：根据代入消元法，可得关于b的高次方程，根据因式分解的方法，可得b2，根据开方运算 可得答案．
解答：解；由
+
=1，得
4b2+9a2=a2b2 ①
由a2-b2=4，得
a2=4+b2 ②
把②代入①，得
4b2+9（4+b2）=（4+b2）b2．
b4-9b2-36=0，
因式分解，得
（b2-12）（b2+3）=0，
解得b2=12，b2=-3（不符合题意的要舍去），
b=±2
；
把b2=12代入②得a2=16，
解得a=±4．
| 4 |
| a2 |
| 9 |
| b2 |
4b2+9a2=a2b2 ①
由a2-b2=4，得
a2=4+b2 ②
把②代入①，得
4b2+9（4+b2）=（4+b2）b2．
b4-9b2-36=0，
因式分解，得
（b2-12）（b2+3）=0，
解得b2=12，b2=-3（不符合题意的要舍去），
b=±2
| 3 |
把b2=12代入②得a2=16，
解得a=±4．
点评：本题考查了高次方程，因式分解降次是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
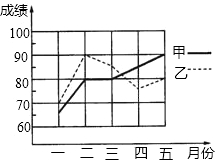为了从甲、乙两名学生中选拔一人代表我校参加今年年底的全区中学生数学竞赛，统计了他们从今年1到5月的每个月的一次测验成绩（单位：分），如图是两人赛前5次测验成绩的折线统计图．