题目内容
1.以下各组线段为边长能组成直角三角形的是( )| A. | 4、5、6 | B. | 2、$\sqrt{2}$、4 | C. | 11、12、13 | D. | 5,12,13 |
分析 根据勾股定理的逆定理可知,当三角形中三边的关系为:a2+b2=c2时,则三角形为直角三角形.
解答 解:A、42+52≠62,不符合勾股定理的逆定理,不能组成直角三角形,故选项错误;
B、22+($\sqrt{2}$)2≠42,不符合勾股定理的逆定理,不能组成直角三角形,故选项错误;
C、112+122≠132,不符合勾股定理的逆定理,不能组成直角三角形,故选项错误;
D、52+122=132,符合勾股定理的逆定理,能组成直角三角形,故选项正确.
故选D.
点评 此题考查的知识点是勾股定理的逆定理,解答此题要用到勾股定理的逆定理:已知三角形ABC的三边满足:a2+b2=c2时,则三角形ABC是直角三角形.解答时,只需看两较小数的平方和是否等于最大数的平方.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
18.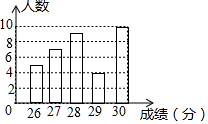 如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )
如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )
 如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )
如图是某校910班参加2017年4月初中升学体育考试成绩(满分30分)的统计图,则该班这次体育升学考试成绩的中位数,众数分别是( )| A. | 28分,30分 | B. | 28.5分,30分 | C. | 27.5分,28分 | D. | 28.2分,30分 |
9.若正比例函数y=kx与反比例函数y=$\frac{{k}^{′}}{x}$的一个交点坐标为(-2,3),则另一个交点为( )
| A. | (-2,-3) | B. | (2,3) | C. | (2,-3) | D. | (3,2) |
6.下列等式中成立的是( )
| A. | a4•a=a4 | B. | a6-a3=a3 | C. | (ab2)3=a3•b5 | D. | (a3)2=a6 |
13.等式(-x2-y2)( )=y4-x4成立,括号内应填入下式中的( )
| A. | x2-y2 | B. | y2-x2 | C. | -x2-y2 | D. | x2+y2 |
11.若分式$\frac{2}{x+3}$有意义,则x的取值范围是( )
| A. | x≠-3 | B. | x≠3 | C. | x>-3 | D. | x<-3 |
 如图:已知△ABC中,AD是中线,且∠1=∠2,求证:AB=AC.
如图:已知△ABC中,AD是中线,且∠1=∠2,求证:AB=AC.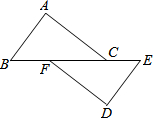 已知:如图,点B,F,C,E在一条直线上,BC=EF,AC=DF,且AC∥DF.
已知:如图,点B,F,C,E在一条直线上,BC=EF,AC=DF,且AC∥DF. 定义:三边长和面积都是整数的三角形称为“整数三角形”.
定义:三边长和面积都是整数的三角形称为“整数三角形”.