Question

13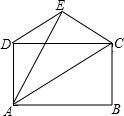．如图，已知四边形ABCD是矩形，把矩形沿直线AC折叠，点B落在E处，连接DE，若$\frac{DE}{AC}$=$\frac{1}{3}$，则$\frac{AD}{AB}$的值为$\frac{\sqrt{2}}{2}$．

Answer 1

分析 首先证明DE∥AC，得到$\frac{DE}{AC}$=$\frac{DO}{OC}$=$\frac{1}{3}$，设OD=OE=a，则OA=OC=3a，求出AD、AB即可解决问题．

解答 解：设AE交CD于点O．
∵四边形ABCD是矩形，
∴AB=DC，AD=BC，∠B=90°，CD∥AB，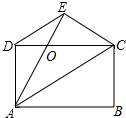
∵△ACE是由△ABC翻折得到，
∴EC=BC=AD，∠BAC=∠CAE=∠DCA，AE=AB=CD，
∴OA=OC，DO=EO，
∴∠OAC=∠OCA=∠ODE=∠OED，
∴DE∥AC，
∴$\frac{DE}{AC}$=$\frac{DO}{OC}$=$\frac{1}{3}$，设OD=OE=a，则OA=OC=3a，
∴AD=EC=$\sqrt{O{C}^{2}-O{E}^{2}}$=2$\sqrt{2}$a，CD=AB=4a，
∴$\frac{AD}{AB}$=$\frac{2\sqrt{2}a}{4a}$=$\frac{\sqrt{2}}{2}$．
故答案为$\frac{\sqrt{2}}{2}$．

点评 本题考查翻折变换、矩形的性质、等腰三角形的性质、平行线的判定等知识，解题的关键是熟练应用这些知识解决问题，学会时参数解决问题，是由中考常考题型．