题目内容
5.已知点A在反比例函数y=$\frac{6}{x}$第一象限的图象上,B(1,0),C(m,0)在x轴上,D是平面上的一点,若以点A,B,C,D为顶点的四边形是正方形,那么m=7或-5.分析 由条件可求得A点坐标,则可求得AB的长,由正方形的性质可得到AB=BC,则可得到关于m的方程,可求得m的值.
解答 解:
∵以点A,B,C,D为顶点的四边形是正方形,
∴AB⊥BC,AB=BC,
∵B(1,0),
∴A点横坐标为1,
∵点A在反比例函数y=$\frac{6}{x}$第一象限的图象上,
∴可求得A点纵坐标为6,
∴AB=6,
∵B(1,0),C(m,0)在x轴上,
∴BC=|m-1|,
∴|m-1|=6,解得m=7或m=-5,
故答案为:7或-5.
点评 本题主要考查反比例函数图象上点的坐标特征,求得A点的坐标是解题的关键.

练习册系列答案
相关题目
15.下列命题中,正确的是( )
| A. | 平行四边形的对角线相等 | B. | 矩形的对角线互相垂直 | ||
| C. | 菱形的对角线互相垂直且平分 | D. | 对角线相等的四边形是正方形 |
17. y关于x的一次函数y=kx+b的图象如图所示,则关于x的不等式kx+b<2的解集是( )
y关于x的一次函数y=kx+b的图象如图所示,则关于x的不等式kx+b<2的解集是( )
 y关于x的一次函数y=kx+b的图象如图所示,则关于x的不等式kx+b<2的解集是( )
y关于x的一次函数y=kx+b的图象如图所示,则关于x的不等式kx+b<2的解集是( )| A. | x<0 | B. | x>1 | C. | x<-4 | D. | x>-4 |
 画图题:如图,画出△ABC的高AD,中线BE,角平分线CF.
画图题:如图,画出△ABC的高AD,中线BE,角平分线CF.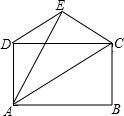 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在E处,连接DE,若$\frac{DE}{AC}$=$\frac{1}{3}$,则$\frac{AD}{AB}$的值为$\frac{\sqrt{2}}{2}$.
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在E处,连接DE,若$\frac{DE}{AC}$=$\frac{1}{3}$,则$\frac{AD}{AB}$的值为$\frac{\sqrt{2}}{2}$. 如图,点A、B在反比例函数y=$\frac{k+1}{x}$的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k+1}{x}$的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( ) 如图在△ABC中,以AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF利用旋转的观点,在此题中,△ADC绕着A点旋转90度可以得到△ABF.
如图在△ABC中,以AB、AC为边分别作正方形ADEB、ACGF,连接DC、BF利用旋转的观点,在此题中,△ADC绕着A点旋转90度可以得到△ABF.