题目内容
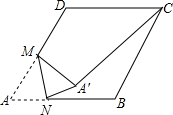如图，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上的一动点，将△AMN沿MN所在直线翻折得到△A′MN，连接A′C，则A′C长度的最小值是考点：菱形的性质,翻折变换（折叠问题）
专题：
分析：根据题意得出A′的位置，进而利用锐角三角函数关系求出A′C的长即可．
解答：
解：如图所示：∵MA′是定值，A′C长度取最小值时，即A′在MC上时，
过点M作MF⊥DC于点F，
∵在边长为2的菱形ABCD中，∠A=60°，M为AD中点，
∴2MD=AD=CD=2，∠FDM=60°，
∴∠FMD=30°，
∴FD=
MD=
，
∴FM=DM×cos30°=
，
∴MC=
=
，
∴A′C=MC-MA′=
-1．
故答案为：
-1．
解：如图所示：∵MA′是定值，A′C长度取最小值时，即A′在MC上时，过点M作MF⊥DC于点F，
∵在边长为2的菱形ABCD中，∠A=60°，M为AD中点，
∴2MD=AD=CD=2，∠FDM=60°，
∴∠FMD=30°，
∴FD=
| 1 |
| 2 |
| 1 |
| 2 |
∴FM=DM×cos30°=
| ||
| 2 |
∴MC=
| FM2+CF2 |
| 7 |
∴A′C=MC-MA′=
| 7 |
故答案为：
| 7 |
点评：此题主要考查了菱形的性质以及锐角三角函数关系等知识，得出A′点位置是解题关键．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，抛物线y=ax2+bx-4与x轴交于点A（-2，0）和点B，与y轴交于点C，直线x=1是该抛物线的对称轴．
如图，已知两个反比例函数
如图，已知在Rt△OAC中，O为坐标原点，直角顶点C在x轴的正半轴上，反比例函数y=
如图，AB是半圆的直径，点O为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E，交⊙O于D，连接BE．设∠BEC=α，则sinα的值为