题目内容
 如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=
如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=| k |
| x |
考点:相似三角形的性质,反比例函数图象上点的坐标特征
专题:数形结合
分析:设OC=a,根据点D在反比例函数图象上表示出CD,再根据相似三角形对应边成比例列式求出AC,然后根据中点的定义表示出点B的坐标,再根据点B在反比例函数图象上表示出a、k的关系,然后用a表示出点B的坐标,再利用待定系数法求一次函数解析式解答.
解答:解:设OC=a,
∵点D在y=
上,
∴CD=
,
∵△OCD∽△ACO,
∴
=
,
∴AC=
=
,
∴点A(a,
),
∵点B是OA的中点,
∴点B的坐标为(
,
),
∵点B在反比例函数图象上,
∴
=
,
∴
=2k2,
∴a4=4k2,
解得,a2=2k,
∴点B的坐标为(
,a),
设直线OA的解析式为y=mx,
则m•
=a,
解得m=2,
所以,直线OA的解析式为y=2x.
故答案为:y=2x.
∵点D在y=
| k |
| x |
∴CD=
| k |
| a |
∵△OCD∽△ACO,
∴
| OC |
| CD |
| AC |
| OC |
∴AC=
| OC2 |
| CD |
| a3 |
| k |
∴点A(a,
| a3 |
| k |
∵点B是OA的中点,
∴点B的坐标为(
| a |
| 2 |
| a3 |
| 2k |
∵点B在反比例函数图象上,
∴
| k | ||
|
| a3 |
| 2k |
∴
| a4 |
| 2 |
∴a4=4k2,
解得,a2=2k,
∴点B的坐标为(
| a |
| 2 |
设直线OA的解析式为y=mx,
则m•
| a |
| 2 |
解得m=2,
所以,直线OA的解析式为y=2x.
故答案为:y=2x.
点评:本题考查了相似三角形的性质,反比例函数图象上点的坐标特征,用OC的长度表示出点B的坐标是解题的关键,也是本题的难点.

练习册系列答案
相关题目
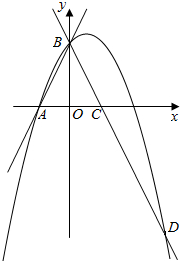 如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).
如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把△AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).
 如图,∠AOB=45°,点O1在OA上,OO1=7,⊙O1的半径为2,点O2在射线OB上运动,且⊙O2始终与OA相切,当⊙O2和⊙O1相切时,⊙O2的半径等于
如图,∠AOB=45°,点O1在OA上,OO1=7,⊙O1的半径为2,点O2在射线OB上运动,且⊙O2始终与OA相切,当⊙O2和⊙O1相切时,⊙O2的半径等于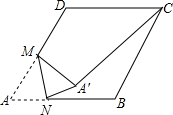 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是
如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是