题目内容
14. 如图,有一电线杆AB直立于地面,它的影子正好射在地面BC段和与地面成45°角的土坡CD上,已知∠BAD=60°,BC=8米,CD=2$\sqrt{2}$米,求电线杆AB的高.(结果保留3个有效数字,$\sqrt{3}$≈1.732)
如图,有一电线杆AB直立于地面,它的影子正好射在地面BC段和与地面成45°角的土坡CD上,已知∠BAD=60°,BC=8米,CD=2$\sqrt{2}$米,求电线杆AB的高.(结果保留3个有效数字,$\sqrt{3}$≈1.732)
分析 构造∠B为直角,∠A为一内角的直角三角形,由CD长易得CE,DE长,在直角三角形DEF中利用30°在正切值可求得EF的长,那么可求得线段BF的长,在直角三角形ABF中利用30°的正切值可求得电线杆AB的高.
解答 解:延长AD交BE的延长线于点F,则∠F=30°,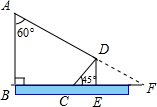
∵∠DCE=45°,DE⊥CF,CD=2 $\sqrt{2}$米,
∴CE=DE=2,
在直角三角形DEF中,EF=$\frac{DE}{tan30°}$=2 $\sqrt{3}$米,
∴BF=BC+CE+EF=(10+2 $\sqrt{3}$)米,
在直角三角形ABF中,AB=BF×tan30°=$\frac{10\sqrt{3}}{3}$+2≈7.77米.
点评 本题考查解直角三角形、锐角三角函数等知识,把四边形的问题转换为特殊三角形利用相应的锐角三角函数知识进行解决是常用的解决问题的方法.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 已知∠1=70°,∠CDN=125°,CM平分∠DCF.试说明:CM∥DN.
已知∠1=70°,∠CDN=125°,CM平分∠DCF.试说明:CM∥DN.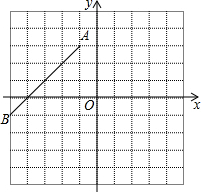 已知,如图平面直角坐标系内,O为坐标原点,A(-1,3),B(-5,-1),连接AB,
已知,如图平面直角坐标系内,O为坐标原点,A(-1,3),B(-5,-1),连接AB,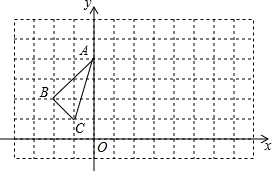
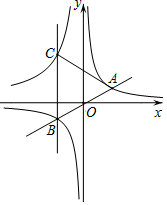 如图,过点O的直线AB与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,A(2,1),直线BC∥y轴,与反比例函数y=$\frac{-3k}{x}$(x<0)的图象交于点C,连接AC,则△ABC的面积为8.
如图,过点O的直线AB与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,A(2,1),直线BC∥y轴,与反比例函数y=$\frac{-3k}{x}$(x<0)的图象交于点C,连接AC,则△ABC的面积为8.