题目内容
14.已知⊙O过点D(3,4),点H与点D关于x轴对称,过H作⊙O的切线交x轴于点A,图1所示.(1)求sin∠HAO的值.
(2)如图2,设⊙O与x轴正半轴交点为F,点B是弧FH上的一个动点(与点H不重合),将射线DB沿DH翻折交⊙O于点C,直线BC交x轴于点G.在点B运动过程中,sin∠OGC的值是否发生变化?并说明你的理由.
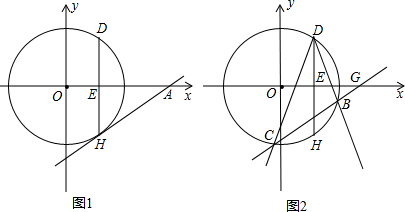
分析 (1)连接OH,利用关于x轴的点的坐标特征得到H(3,-4),再根据切线的性质,由AH与⊙O相切于H得到OH⊥AH,则可利用等角的余角相等得到∠HAO=∠QHO;在Rt△OQH中,根据勾股定理计算出OH=5,然后根据正弦的定义计算出sin∠QHO的值,即sin∠HAO的值可求出;
(2)sin∠OGC的值不变,连结OH,则OH⊥BC,又因为DH⊥OA,所以∠OHE+∠GOH=90°,进而可得∠OGC=∠OHE,所以sin∠OGE=sin∠EHO问题得解.
解答 解:(1)连结OH,
∵AH与⊙O相切于点H,
∴∠OHA=90°,
∵D、H关于x轴对称,D为(3,4),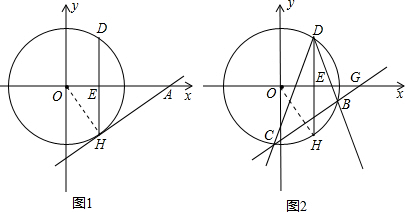
∴DH⊥OA,H为(3.-4),
∴OH=5,∠HAO=∠EHO,
∴sin∠HAO=sin∠EHO=$\frac{OE}{OH}$=$\frac{3}{5}$;
(2)sin∠OGC的值不变.
理由如下:如2图
∵射线DB沿DH翻折交⊙O于点C,
∴∠CDH=∠BDH,
∴弧CH=弧BH,
连结OH,则OH⊥BC,
∴∠OGC+∠GOH=90°,
又∵DH⊥OA,
∴∠OHE+∠GOH=90°,
∴∠OGC=∠OHE,
∴sin∠OGE=sin∠EHO=$\frac{OE}{OH}$=$\frac{3}{5}$.
点评 本题考查了圆的综合题:熟练掌握垂径定理及其推论、圆周角定理和切线的性质;会运用勾股定理和锐角三角函数的定义进行几何计算;理解关于x轴对称的点的坐标特征和坐标与图形性质.

练习册系列答案
相关题目
5. 如图,笑脸盖住的点的坐标可能为( )
如图,笑脸盖住的点的坐标可能为( )
 如图,笑脸盖住的点的坐标可能为( )
如图,笑脸盖住的点的坐标可能为( )| A. | (5,2) | B. | (-2,3) | C. | (-4,-2) | D. | (3,-4) |
3.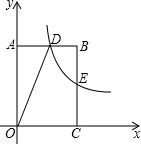 如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若矩形OABC的面积为6,则双曲线的解析式为( )
如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若矩形OABC的面积为6,则双曲线的解析式为( )
 如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若矩形OABC的面积为6,则双曲线的解析式为( )
如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC的中点E,交AB于点D.若矩形OABC的面积为6,则双曲线的解析式为( )| A. | y=$\frac{1}{x}$ | B. | y=$\frac{2}{x}$ | C. | y=$\frac{3}{x}$ | D. | y=$\frac{6}{x}$ |
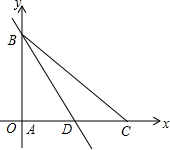 如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.
如图,△ABC中,∠BAC=90°,AB=AC=4,BD是AC边上的中线,分别以AC、AB所在直线为x轴、y轴建立直角坐标系.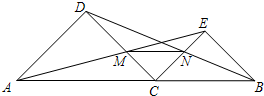 如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N.
如图,已知C是线段AB上的任意一点(除端点外),分别以AC、BC为斜边并且在AB的同一侧作等腰直角△ACD和△BCE,连接AE交CD于点M,连接BD交CE于点N. 如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,试画出一个顶点都在格点上,且面积为5的正方形.
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,试画出一个顶点都在格点上,且面积为5的正方形.