题目内容
3．
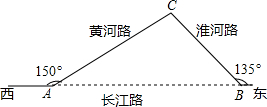如图，已知：长江路西段与黄河路的夹角为150°，长江路东段与淮河路的夹角为135°，黄河路全长AC=20km，从A地道B地必须先走黄河路经C点后再走淮河路才能到达，城市道路改造后，直接打通长江路（即修建AB路段）．问：打通长江路后从A地道B地可少走多少路程？（参考数据：$\sqrt{2}$≈1.4，$\sqrt{3}$≈1.7）
分析 首先过点C作CD⊥AB于点D，分别求出DC，AD，BC，BD的长，进而得出答案．
解答 
解：如图所示：过点C作CD⊥AB于点D，
在Rt△ACD中，∠CAD=30°，AC=20km，
则CD=10km，AD=10$\sqrt{3}$km，
在Rt△BCD中，∠CBD=45°，CD=10km，
故BD=10km，BC=10$\sqrt{2}$km，
则AC+BC-AB=20+10$\sqrt{2}$-10$\sqrt{3}$-10≈7（km），
答：打通长江路后从A地道B地可少走7km的路程．
点评 此题主要考查了解直角三角形的应用，根据题意熟练应用锐角三角函数关系是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
14．下列运算结果正确的是（ ）
| A． | a3+a2=a5 | B． | （x+y）2=x2+y2 | C． | x8÷x2=x4 | D． | （ab）2=a2b2 |
15．-3的绝对值是（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | -3 |
阅读下列材料：
8．
二次函数y=-x2+mx的图象如图，对称轴为直线x=2，若关于x的一元二次方程-x2+mx-t=0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是（ ）
二次函数y=-x2+mx的图象如图，对称轴为直线x=2，若关于x的一元二次方程-x2+mx-t=0（t为实数）在1＜x＜5的范围内有解，则t的取值范围是（ ）| A． | t＞-5 | B． | -5＜t＜3 | C． | 3＜t≤4 | D． | -5＜t≤4 |
