题目内容
11.先化简,再求值:[(a-b)2+(2a+b)(1-b)-b]÷(-$\frac{1}{2}$a),其中a、b满足|a+1|+(2b-1)2=0.分析 根据完全平方公式以及多项式乘多项式的法则化简展开,再根据非负数的性质求出a、b代入即可.
解答 解:原式=(a2-2ab+b2+2a-2ab+b-b2-b)÷(-$\frac{1}{2}$a),
=(a2-4ab+2a)÷(-$\frac{1}{2}$a),
=-2a+8b-4,
∵|a+1|+(2b-1)2=0,
又∵|a+1|≥0,(2b-1)2≥0,
∴a=-1.b=$\frac{1}{2}$,
∴原式=2+4-4=2.
点评 本题考查整式的混合运算,乘法公式,多项式乘多项式法则等整式,解题的关键是灵活运用这些知识解决问题,注意符号问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某校举办初中生演讲比赛,每班派一名学生参赛,现某班有A,B,C三名学生竞选,他们的笔试成绩和口试成绩分别用两种方式进行了统计,如表和图1:

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本年级段的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按3:4:3的比例确定最后成绩,请计算这三名学生的最后成绩,并根据最后成绩判断谁能当选.
| 学生 | A | B | C |
| 笔试成绩(单位:分) | 85 | 95 | 90 |
| 口试成绩(单位:分) | 90 | 80 | 85 |

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本年级段的300名学生代表进行投票,每票计1分,三名候选人的得票情况如图2(没有弃权票,每名学生只能推荐一人),若将笔试、口试、得票三项测试得分按3:4:3的比例确定最后成绩,请计算这三名学生的最后成绩,并根据最后成绩判断谁能当选.
20.反比例函数y=$\frac{k}{2x}$(k为非零常数)的图象在其所在象限内,y的值随x值的增大而增大,那么函数y=$\frac{2}{k}$x的图象经过第( )象限.
| A. | 一、二 | B. | 一、三 | C. | 二、三 | D. | 二、四 |
1.下列命题是假命题的是( )
| A. | 两个角的和等于平角时,这两个角互为补角 | |
| B. | 平行于同一直线的两直线平行 | |
| C. | 垂直于同一直线的两直线平行 | |
| D. | 如果$\frac{a}{c}$=$\frac{b}{c}$那么a=b |
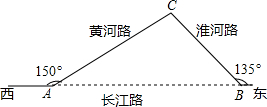 如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)