题目内容
12.(1)计算:(1-$\sqrt{2}$)0-tan60°+(-$\frac{1}{2}$)-1(2)解方程:3(x-1)2=x(x-1)
分析 (1)根据非零的零次幂等于1,负整数指数幂与正整数指数幂互为倒数,特殊角三角函数值,可得答案;
(2)根据因式分解法,可得方程的解.
解答 解:(1)原式=1-$\sqrt{3}$-2=-1-$\sqrt{3}$;
(2)移项,得3(x-1)2-x(x-1)=0,
因式分解,得(x-1)[3(x-1)-x]=0
于是,得(x-1)(2x-3)=0
x-1=0或2x-3=0,
解得x1=1,x2=$\frac{3}{2}$.
点评 本题考查了解一元二次方程,因式分解是解题关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
20.反比例函数y=$\frac{k}{2x}$(k为非零常数)的图象在其所在象限内,y的值随x值的增大而增大,那么函数y=$\frac{2}{k}$x的图象经过第( )象限.
| A. | 一、二 | B. | 一、三 | C. | 二、三 | D. | 二、四 |
7.下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共 8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为( )


| A. | 50 | B. | 64 | C. | 68 | D. | 72 |
4. 随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
请根据统计图中提供的信息,解答下列问题:
(1)本次接受调查的总人数是200人;
(2)通过计算,将条形统计图补充完整;
(3)扇形统计图中,观点“D”的百分比是24%,“B”所对应的圆心角的度数是126°;
(4)估算在全校3000名学生中,对“低头族”表示不赞同的人数.
 随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).| 您如何看待“低头族”的调查问卷 您好!这是一份关于您如何看待低头族的问卷调查表,请在表格内选择一项您最认同的观点,在其后的空格内打对勾,感谢您的参与! | ||
| 代码 | 观点 | 您的选择 |
| A | 获取信息方便 | |
| B | 联系朋友方便 | |
| C | 对视力不好,影响健康 | |
| D | 使朋友亲人疏远,不利于交流 | |
(1)本次接受调查的总人数是200人;
(2)通过计算,将条形统计图补充完整;
(3)扇形统计图中,观点“D”的百分比是24%,“B”所对应的圆心角的度数是126°;
(4)估算在全校3000名学生中,对“低头族”表示不赞同的人数.
1.下列命题是假命题的是( )
| A. | 两个角的和等于平角时,这两个角互为补角 | |
| B. | 平行于同一直线的两直线平行 | |
| C. | 垂直于同一直线的两直线平行 | |
| D. | 如果$\frac{a}{c}$=$\frac{b}{c}$那么a=b |
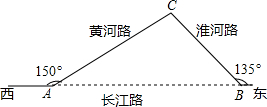 如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
如图,已知:长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).问:打通长江路后从A地道B地可少走多少路程?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)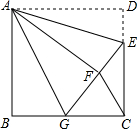 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论: