题目内容
如图，DE∥BC．（1）如果AD=2，DB=3，求DE：BC的值；
（2）如果AD=8，DB=12，AC=15，DE=7，求AE和BC的长．
考点：平行线分线段成比例
专题：
分析：（1）证明△ADE∽△ABC，列出比例式求解即可解决问题．
（2）类比（1），列出比例式求解即可解决问题．
（2）类比（1），列出比例式求解即可解决问题．
解答：解：（1）∵DE∥BC，
∴△ADE∽△ABC，
∴
=
，
而AD=2，DB=3，AB=5，
∴
=
．
（2）由（1）知：△ADE∽△ABC，
∴
=
=
，
而AD=8，DB=12，AC=15，DE=7，
∴
=
=
，
解得：AE=6，BC=
．
解：（1）∵DE∥BC，∴△ADE∽△ABC，
∴
| AD |
| AB |
| DE |
| BC |
而AD=2，DB=3，AB=5，
∴
| DE |
| BC |
| 2 |
| 5 |
（2）由（1）知：△ADE∽△ABC，
∴
| AD |
| AB |
| DE |
| BC |
| AE |
| AC |
而AD=8，DB=12，AC=15，DE=7，
∴
| 8 |
| 20 |
| 7 |
| BC |
| AE |
| 15 |
解得：AE=6，BC=
| 35 |
| 2 |
点评：该题主要考查了平行线分线段成比例定理及其应用问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
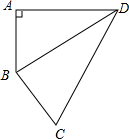如图，四边形ABCD中，∠A=90．，连结对角线BD，BD⊥BC，现测得：AB=9cm，AD=12cm，CD=17cm，求四边形ABCD的面积．
如图，△ABC中，
在四边形ABCD中，∠ABC=90°，AB=BC=4，CD=2，AD=6，求∠BCD的度数．