题目内容
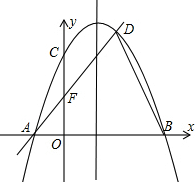 已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A,B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A,B,点B(4,0),抛物线的对称轴为x=1,直线AD交抛物线于点D(2,m).(1)求二次函数的解析式并写出D点坐标;
(2)点E是BD中点,点Q是线段AB上一动点,当△QBE和△ABD相似时,求点Q的坐标.
考点:二次函数综合题,相似三角形的判定与性质
专题:综合题,分类讨论
分析:(1)运用待定系数法就可求出二次函数的解析式,然后把点D(2,m)代入二次函数的解析式,就可求出点D的坐标;
(2)过点D作DH⊥AB于点H,如图,根据勾股定理可求出BD,易求出点A的坐标,从而得到AB长,然后分两种情况(①若△QBE∽△ABD,②若△QBE∽△DBA)讨论,只需运用相似三角形的性质就可求出BQ,从而得到OQ,即可得到点Q的坐标.
(2)过点D作DH⊥AB于点H,如图,根据勾股定理可求出BD,易求出点A的坐标,从而得到AB长,然后分两种情况(①若△QBE∽△ABD,②若△QBE∽△DBA)讨论,只需运用相似三角形的性质就可求出BQ,从而得到OQ,即可得到点Q的坐标.
解答:解:(1)由题可得:
,
解得:
,
∴二次函数的解析式为y=-
x2+x+4.
∵点D(2,m)在抛物线上,
∴m=-
×22+2+4=4,
∴点D的坐标为(2,4).
(2)过点D作DH⊥AB于点H,如图,
∵点D(2,4),点B(4,0),
∴DH=4,OH=2,OB=4,
∴BH=2,∴DB=
=2
.
∵点E为DB的中点,
∴BE=
BD=
.
令y=0得-
x2+x+4=0,
解得:x1=4,x2=-2,
∴点A为(-2,0),
∴AB=4-(-2)=6.
①若△QBE∽△ABD,
则
=
,
∴
=
,
解得:BQ=3,
∴OQ=OB-BQ=4-3=1,
∴点Q的坐标为(1,0);
②若△QBE∽△DBA,
则
=
,
∴
=
,
∴BQ=
,
∴OQ=OB-BQ=4-
=
,
∴点Q的坐标为(
,0).
综上所述:点Q的坐标为(1,0)或(
,0).
|
解得:
|
∴二次函数的解析式为y=-
| 1 |
| 2 |
∵点D(2,m)在抛物线上,
∴m=-
| 1 |
| 2 |
∴点D的坐标为(2,4).
(2)过点D作DH⊥AB于点H,如图,
∵点D(2,4),点B(4,0),
∴DH=4,OH=2,OB=4,
∴BH=2,∴DB=
| DH2+HB2 |
| 5 |
∵点E为DB的中点,
∴BE=
| 1 |
| 2 |
| 5 |
令y=0得-
| 1 |
| 2 |
解得:x1=4,x2=-2,
∴点A为(-2,0),
∴AB=4-(-2)=6.
①若△QBE∽△ABD,

则
| BQ |
| BA |
| BE |
| BD |
∴
| BQ |
| 6 |
| ||
2
|
解得:BQ=3,
∴OQ=OB-BQ=4-3=1,
∴点Q的坐标为(1,0);
②若△QBE∽△DBA,
则
| BQ |
| BD |
| BE |
| BA |
∴
| BQ | ||
2
|
| ||
| 6 |
∴BQ=
| 5 |
| 3 |
∴OQ=OB-BQ=4-
| 5 |
| 3 |
| 7 |
| 3 |
∴点Q的坐标为(
| 7 |
| 3 |
综上所述:点Q的坐标为(1,0)或(
| 7 |
| 3 |
点评:本题主要考查了用待定系数法求二次函数的解析式、二次函数图象上点的坐标特征、相似三角形的判定与性质、勾股定理等知识,运用相似三角形的性质及分类讨论是解决第(2)小题的关键.

练习册系列答案
相关题目
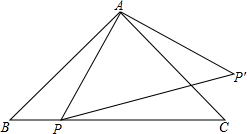 如图,△ABC是等腰三角形,点P是斜边AB上一点,将△CAP绕点C逆时针旋转90°至△CBP′的位置,若AC=2
如图,△ABC是等腰三角形,点P是斜边AB上一点,将△CAP绕点C逆时针旋转90°至△CBP′的位置,若AC=2 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=8,ON,CD分别为两圆的半径,求阴影部分的面积.
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=8,ON,CD分别为两圆的半径,求阴影部分的面积. 用直尺和圆规作一个角等于∠MON.(不写步骤,保留作图痕迹)
用直尺和圆规作一个角等于∠MON.(不写步骤,保留作图痕迹)