题目内容
2.尝试练习:(1)$\frac{3b}{x}$+$\frac{b}{x}$
(2)$\frac{{x}^{2}}{x-2}$-$\frac{4}{x-2}$
(3)$\frac{2y}{x-1}$-$\frac{3y+1}{1-x}$-$\frac{y}{x-1}$
(4)$\frac{6x}{5x-7}$-$\frac{3x-8}{7-5x}$+$\frac{-x+6}{7-5x}$.
分析 (1)把分母相加为4b,分子不变;
(2)把分母相加为x2-4,再分解因式为(x+2)(x-2),约分即可;
(3)先把第二个分式-$\frac{3y+1}{1-x}$化为+$\frac{3y+1}{x-1}$,再加减;
(4)把第二个分式和第三个分式的分母化为5x-7,再加减.
解答 解:(1)$\frac{3b}{x}$+$\frac{b}{x}$,
=$\frac{3b+b}{x}$,
=$\frac{4b}{x}$;
(2)$\frac{{x}^{2}}{x-2}$-$\frac{4}{x-2}$,
=$\frac{{x}^{2}-4}{x-2}$,
=$\frac{(x+2)(x-2)}{x-2}$,
=x+2;
(3)$\frac{2y}{x-1}$-$\frac{3y+1}{1-x}$-$\frac{y}{x-1}$,
=$\frac{2y}{x-1}$+$\frac{3y+1}{x-1}$-$\frac{y}{x-1}$,
=$\frac{2y+3y+1-y}{x-1}$,
=$\frac{4y+1}{x-1}$;
(4)$\frac{6x}{5x-7}$-$\frac{3x-8}{7-5x}$+$\frac{-x+6}{7-5x}$,
=$\frac{6x}{5x-7}$+$\frac{3x-8}{5x-7}$+$\frac{x-6}{5x-7}$,
=$\frac{6x+3x-8+x-6}{5x-7}$,
=$\frac{10x-14}{5x-7}$,
=$\frac{2(5x-7)}{5x-7}$,
=2.
点评 本题考查了分式的加减法,熟练掌握分式加减法法则是关键:先化为同分母分式,再加减;注意互为相反数化为相等时,提取负号,如7-5x=-(5x-7),在分式的加减法时,要注意分解因式后再约分.

| A. | -2x2y | B. | -3xy2 | C. | 2x3y | D. | 5xy |
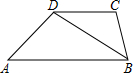 如图所示,在梯形ABCD中,AB∥CD,BD2=AB•DC,求证:∠A=∠CBD.
如图所示,在梯形ABCD中,AB∥CD,BD2=AB•DC,求证:∠A=∠CBD. 如图所示,将直径AB=6的半圆绕着点A逆时针旋转30°,此时点B落到点C处,图中阴影部分的面积是3π.
如图所示,将直径AB=6的半圆绕着点A逆时针旋转30°,此时点B落到点C处,图中阴影部分的面积是3π.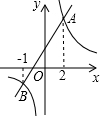 如图,一次函数y=kx+b(k、b为常数,且k≠0)的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点.则关于x的方程kx+b=$\frac{m}{x}$的解为-1和2.
如图,一次函数y=kx+b(k、b为常数,且k≠0)的图象与反比例函数y=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A、B两点.则关于x的方程kx+b=$\frac{m}{x}$的解为-1和2. 已知,如图,∠BAG=45°,∠AGD=135°,∠E=∠F.求证:∠BAE=∠CGF.
已知,如图,∠BAG=45°,∠AGD=135°,∠E=∠F.求证:∠BAE=∠CGF.