题目内容
11.已知a,b,c是△ABC的三条边长,且关于x的方程(c-b)x2+2(b-a)x+(a-b)=0有两个相等的实数根,那么这个三角形是( )| A. | 等边三角形 | B. | 腰和底不等的等腰三角形 | ||
| C. | 不等边三角形 | D. | 直角三角形 |
分析 根据方程(c-b)x2+2(b-a)x+(a-b)=0有两个相等的实数根结合根的判别式以及二次项系数非0,即可得出△ABC是腰和底不等的等腰三角形,此题得解.
解答 解:∵关于x的方程(c-b)x2+2(b-a)x+(a-b)=0有两个相等的实数根,
∴$\left\{\begin{array}{l}{c-b≠0}\\{△=[2(b-a)]^{2}-4(c-b)(a-b)=0}\end{array}\right.$,
解得:a=b或a=c(且b≠c),
∵a,b,c是△ABC的三条边长,
∴△ABC是腰和底不等的等腰三角形.
故选B.
点评 本题考查了根的判别式以及等腰三角形的判定,根据根的判别式得出a=b或a=c(且b≠c)是解题的关键.

练习册系列答案
相关题目
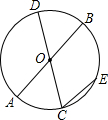 如图,已知AB和CD为⊙O的两条直径,弦CE∥AB,$\widehat{EC}$的度数为40°,求∠BOD的度数.
如图,已知AB和CD为⊙O的两条直径,弦CE∥AB,$\widehat{EC}$的度数为40°,求∠BOD的度数.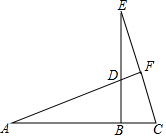 已知:A、B、C在同一直线上,BE⊥AC,AB=BE,AD=CE,求证:
已知:A、B、C在同一直线上,BE⊥AC,AB=BE,AD=CE,求证: