题目内容
6.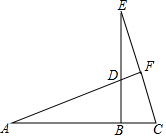 已知:A、B、C在同一直线上,BE⊥AC,AB=BE,AD=CE,求证:
已知:A、B、C在同一直线上,BE⊥AC,AB=BE,AD=CE,求证:①∠A=∠E;
②AF⊥CE.
分析 ①由HL证明Rt△ABD≌Rt△EBC,得出∠A=∠E即可;
②由全等三角形的性质得出∠ADB=∠C,由角的互余关系得出∠A+∠C=90°,求出∠AFC=90°,即可得出结论.
解答 证明:∵BE⊥AC,
∴∠ABD=∠EBC=90°,
在Rt△ABD和Rt△EBC中,$\left\{\begin{array}{l}{AD=EC}&{\;}\\{AB=EB}&{\;}\end{array}\right.$,
∴Rt△ABD≌Rt△EBC(HL),
∴∠A=∠E;
②∵Rt△ABD≌Rt△EBC,
∴∠ADB=∠C,
∵∠C+∠E=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,
即AF⊥CE.
点评 本题考查了全等三角形的判定与性质、直角三角形的性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
4.无论b取何值,抛物线y=a(x-b)2+b的图象顶点都在( )
| A. | x轴上 | B. | y轴上 | ||
| C. | 第一、三象限的平分线上 | D. | 第二、四象限的平分线上 |
11.已知a,b,c是△ABC的三条边长,且关于x的方程(c-b)x2+2(b-a)x+(a-b)=0有两个相等的实数根,那么这个三角形是( )
| A. | 等边三角形 | B. | 腰和底不等的等腰三角形 | ||
| C. | 不等边三角形 | D. | 直角三角形 |