题目内容
13.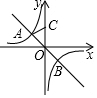 如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )
如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
分析 联立正、反比例函数解析式成方程组,解之可求出点A、B的坐标,进而可得出OB=2,再根据OC=OB结合三角形的面积公式即可得出结论.
解答 解:联立正、反比例函数解析式成方程组,
$\left\{\begin{array}{l}{y=-x}\\{y=-\frac{2}{x}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-\sqrt{2}}\\{{y}_{1}=\sqrt{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\sqrt{2}}\\{{y}_{2}=-\sqrt{2}}\end{array}\right.$,
∴点A的坐标为(-$\sqrt{2}$,$\sqrt{2}$),点B的坐标为($\sqrt{2}$,-$\sqrt{2}$).
∴OB=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2.
∵OC=OB,
∴S△AOC=$\frac{1}{2}$OC•|xA|=$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$.
故选D.
点评 本题考查了反比例函数与一次函数的交点问题以及三角形的面积,联立正、反比例函数解析式成方程组求出两函数图象的交点坐标是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知一个坡的坡比为i,坡角为α,则下列等式成立的是( )
| A. | i=sinα | B. | i=cosα | C. | i=tanα | D. | i=cotα |
8.点P(2,1)关于原点对称的点的坐标是( )
| A. | (-2,-1) | B. | (-1,-2) | C. | (2,-1) | D. | (-2,1) |
5.定义运算$\frac{a}{b}$=$\frac{a+1}{b+1}$,若a≠-1,b≠-1,则下列等式中不正确的是( )
| A. | $\frac{a}{b}$×$\frac{b}{a}$=1 | B. | $\frac{b}{a}$+$\frac{c}{a}$=$\frac{b+c}{a}$ | ||
| C. | ($\frac{a}{b}$)2=$\frac{({a}^{2}+2a)}{({b}^{2}+2b)}$ | D. | $\frac{a}{a}$=1 |
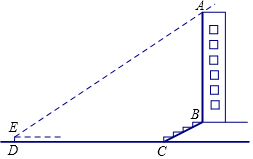 某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)
某校兴趣小组想测量一座大楼AB的高度.如图,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:$\sqrt{3}$.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米)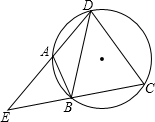 如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E,若∠BDC=a,则∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)
如图,点A、B、C、D在同一个圆上,DB=DC,DA、CB的延长线相交于点E,若∠BDC=a,则∠EAB=90°-$\frac{1}{2}$α(用含a的式子表示)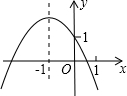 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
已知二次函数y=ax2+bx+c的图象如图所示,有以下结论: 如图是由若干个边长为1个单位长度的小正方形组成的网格图,已知四边形ABCD在网图的格点上.按要求完成下列各小题.
如图是由若干个边长为1个单位长度的小正方形组成的网格图,已知四边形ABCD在网图的格点上.按要求完成下列各小题.