如图是由若干个边长为1个单位长度的小正方形组成的网格图.已知四边形ABCD在网图的格点上．按要求完成下列各小题．(1)求作四边形A1B1C1D1.使得四边形A1B1C1D1与四边形ABCD关于点O成中心对称图形,的基础上.连接A1D.求A1D的长度．题目和参考答案——青夏教育精英家教网—

题目内容

3．

如图是由若干个边长为1个单位长度的小正方形组成的网格图，已知四边形ABCD在网图的格点上．按要求完成下列各小题．
（1）求作四边形A₁B₁C₁D₁，使得四边形A₁B₁C₁D₁与四边形ABCD关于点O成中心对称图形；
（2）在（1）的基础上，连接A₁D，求A₁D的长度．

分析（1）分别作出各点关于点O的对称点，再顺次连接即可；
（2）连接A₁D，利用勾股定理即可得出结论．

解答解：（1）如图，四边形A₁B₁C₁D₁与即为所求；

（2）A₁D=$\sqrt{{4}^{2}+{7}^{2}}$=$\sqrt{65}$．

点评本题考查的是作图-旋转变换，熟知图形旋转的性质是解答此题的关键．

练习册系列答案

相关题目

13．

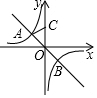如图，直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A，B，点C在y轴的正半轴上，且OC=OB，则△AOC的面积为（　　）

14．

如图，把△ABC沿AB边平移到△A′B′C′的位置，它们重叠部分（即图中阴影部分）的面积是△ABC面积的$\frac{1}{4}$，若AB=2，则△ABC平移的距离是1．

11．不等式组$\left\{\begin{array}{l}{x-1＜3}\\{x+1＞3}\end{array}\right.$的解集是（　　）

18．水是地球表面最多的分子，一个水分子由两个氢原子核一个氧原子构成，美国水分子的直径是0.0000000004m，将数字0.0000000004用科学记数法表示为4×10^-10．

8．因式分解．
（1）3a（a+b）-5（a+b）
（2）x³y²-x⁵．

15．计算：（-2a²b³）⁵÷（-2a³b⁴）³×$\frac{1}{2}$ab．

14．比较大小：-4＜-2，4的相反数是-4．-5的倒数是-0.2．

15．关于x的一元二次方程（a-1）x²+x+a²-1=0的一个根是0，则a的值为（　　）

试题分类