题目内容
5.定义运算$\frac{a}{b}$=$\frac{a+1}{b+1}$,若a≠-1,b≠-1,则下列等式中不正确的是( )| A. | $\frac{a}{b}$×$\frac{b}{a}$=1 | B. | $\frac{b}{a}$+$\frac{c}{a}$=$\frac{b+c}{a}$ | ||
| C. | ($\frac{a}{b}$)2=$\frac{({a}^{2}+2a)}{({b}^{2}+2b)}$ | D. | $\frac{a}{a}$=1 |
分析 根据定义:$\frac{a}{b}$=$\frac{a+1}{b+1}$,一一计算即可判断.
解答 解:A、正确.∵$\frac{a}{b}$=$\frac{a+1}{b+1}$,$\frac{b}{a}$=$\frac{b+1}{a+1}$.
∴$\frac{a}{b}$×$\frac{b}{a}$=$\frac{a+1}{b+1}$×$\frac{b+1}{a+1}$=1.
B、错误.$\frac{b}{a}$+$\frac{c}{a}$=$\frac{b+1}{a+1}$+$\frac{c+1}{a+1}$=$\frac{b+c+2}{a+1}$.
C、正确.∵($\frac{a}{b}$)2=($\frac{a+1}{b+1}$)2=$\frac{{a}^{2}+2a+1}{{b}^{2}+2a+1}$=$\frac{{a}^{2}+2a}{{b}^{2}+2b}$.
D、正确.$\frac{a}{a}$=$\frac{a+1}{a+1}$=1.
故选B.
点评 本题考查分式的运算,理解题意是解题的关键是,学会根据定义的运算法则进行计算,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列说法正确的是( )
| A. | 投掷一枚均匀的硬币,正面朝上的概率是$\frac{1}{2}$ | |
| B. | 投掷一枚图钉,钉尖朝上、朝下的概率一样 | |
| C. | 投掷一枚均匀的骰子,每一种点数出现的概率都是$\frac{1}{6}$,所以每投6次,一定会出现一次“l点” | |
| D. | 投掷一枚均匀的骰子前默念几次“出现6点”,投掷结果“出现6点”的可能性就会加大 |
13.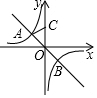 如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )
如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )
 如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )
如图,直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A,B,点C在y轴的正半轴上,且OC=OB,则△AOC的面积为( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
10. 如图,⊙O的半径为3,PA、PB分别切⊙O于点A、B,OP=6,则PB的长为( )
如图,⊙O的半径为3,PA、PB分别切⊙O于点A、B,OP=6,则PB的长为( )
 如图,⊙O的半径为3,PA、PB分别切⊙O于点A、B,OP=6,则PB的长为( )
如图,⊙O的半径为3,PA、PB分别切⊙O于点A、B,OP=6,则PB的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
 如图,直线y1=2x+2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$交于C、D两点,且DA=AB=BC.
如图,直线y1=2x+2与坐标轴交于A、B两点,与双曲线y2=$\frac{k}{x}$交于C、D两点,且DA=AB=BC. 如图,把△ABC沿AB边平移到△A′B′C′的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{4}$,若AB=2,则△ABC平移的距离是1.
如图,把△ABC沿AB边平移到△A′B′C′的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{4}$,若AB=2,则△ABC平移的距离是1.