题目内容
18．
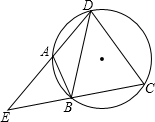如图，点A、B、C、D在同一个圆上，DB=DC，DA、CB的延长线相交于点E，若∠BDC=a，则∠EAB=90°-$\frac{1}{2}$α（用含a的式子表示）
分析 先根据等腰三角形的性质求出∠C的度数，再由圆内接四边形的性质即可得出结论．
解答 解：∵DB=DC，∠BDC=α，
∴∠C=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α．
∵四边形ABCD内接是圆内接四边形，、
∴∠EAB=∠C=90°-$\frac{1}{2}$α．
故答案为：90°-$\frac{1}{2}$α．
点评 本题考查的是圆内接四边形的性质，熟知圆内接四边形的对角互补是解答此题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．如果向量$\overrightarrow a$、$\overrightarrow b$、$\overrightarrow x$满足$\overrightarrow x$+$\overrightarrow a$=$\frac{3}{2}$（$\overrightarrow a$-$\frac{2}{3}$$\overrightarrow b$），那么$\overrightarrow x$用$\overrightarrow a$、$\overrightarrow b$表示正确的是（ ）
| A． | $\overrightarrow a-2\overrightarrow b$ | B． | $\frac{5}{2}\overrightarrow a-\overrightarrow b$ | C． | $\overrightarrow a-\frac{2}{3}\overrightarrow b$ | D． | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ |
6．与-$\frac{5}{4}$互为相反数的是（ ）
| A． | -$\frac{4}{5}$ | B． | -$\frac{5}{4}$ | C． | $\frac{5}{4}$ | D． | $\frac{4}{5}$ |
13．
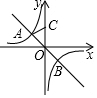如图，直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A，B，点C在y轴的正半轴上，且OC=OB，则△AOC的面积为（ ）
如图，直线y=-x与双曲线y=-$\frac{2}{x}$相交于点A，B，点C在y轴的正半轴上，且OC=OB，则△AOC的面积为（ ）| A． | 2$\sqrt{2}$ | B． | 2 | C． | $\frac{\sqrt{2}}{2}$ | D． | $\sqrt{2}$ |
3．如果2x3my4与-3x9y2n是同类项，那么m、n的值分别为（ ）
| A． | m=-3，n=2 | B． | m=3，n=2 | C． | m=-2，n=3 | D． | m=2，n=3 |
10．
如图，⊙O的半径为3，PA、PB分别切⊙O于点A、B，OP=6，则PB的长为（ ）
如图，⊙O的半径为3，PA、PB分别切⊙O于点A、B，OP=6，则PB的长为（ ）| A． | 3 | B． | 2$\sqrt{3}$ | C． | 3$\sqrt{3}$ | D． | 6 |
如图所示，已知函数y1=$\frac{k}{x}$（x＞0）的图象与一次函数y2=-x+3的图象交于A（1，m），B（2，n）两点．