题目内容
6.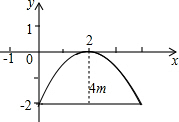 某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.
某次军事学习时,我军挖了一个横截面为抛物线的防空洞,尺寸如图.(1)求该抛物线的解析式;
(2)若士兵身高为1.60米,则在他不弯腰的情况下,在洞内横向活动范围有几米?
分析 (1)利用待定系数法求出函数解析式进而得出答案;
(2)利用所求函数解析式进而得出y=1.6m时,x的值进而得出答案.
解答 解:(1)设抛物线解析式为:y=a(x-2)2,
将(0,-2)代入得出:a=-$\frac{1}{2}$,
故抛物线的解析式为:y=-$\frac{1}{2}$(x-2)2;
(2)士兵身高为1.60米,即当y=-0.4时,-0.4=-$\frac{1}{2}$(x-2)2
解得:x1=2+$\frac{2\sqrt{5}}{5}$,x2=2-$\frac{2\sqrt{5}}{5}$,
故2+$\frac{2\sqrt{5}}{5}$-(2-$\frac{2\sqrt{5}}{5}$)=$\frac{4\sqrt{5}}{5}$(m),
答:士兵身高为1.60米,则在他不弯腰的情况下,在洞内横向活动范围有$\frac{4\sqrt{5}}{5}$米.
点评 此题主要考查了二次函数的应用,正确求出函数解析式是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
15.设a是任意有理数,下列说法正确的是( )
| A. | (a+1)2的值总是正的 | B. | a2+1的值总是正的 | ||
| C. | -(a+1)2的值总是负的 | D. | a2+1的值中,最大值是1 |
 已知,如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB交BC于E.
已知,如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB交BC于E.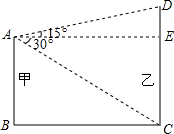 如图,平地上有甲乙两楼,甲楼高15米.已知从甲楼顶测得乙楼底的俯角为30°,又测得乙楼顶的仰角为15°.求乙楼的高.(tan15°=0.2679,精确到0.01)
如图,平地上有甲乙两楼,甲楼高15米.已知从甲楼顶测得乙楼底的俯角为30°,又测得乙楼顶的仰角为15°.求乙楼的高.(tan15°=0.2679,精确到0.01) 如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.
如图,⊙O直径AB与弦CD相交于E,∠AED=60°,AE=3,BE=7,求CD长.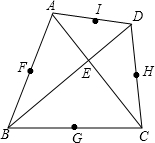 已知:如图,四边形ABCD的对角线AC⊥BD,垂足为E,点F,G,H,I分别是四边形各边中点.求证:F,G,H,I四个点在同一个圆上.
已知:如图,四边形ABCD的对角线AC⊥BD,垂足为E,点F,G,H,I分别是四边形各边中点.求证:F,G,H,I四个点在同一个圆上. 如图,平面直角坐标系中,一直线l分别交x轴、y轴于点B,C,过点C作直线l的垂线交x轴于点A.若点A的坐标为(2,0)且AC=4,则在直线l上是否存在点P,使△PAB与△BOC相似?若存在,请求出该点坐标;若不存在,请说明理由.
如图,平面直角坐标系中,一直线l分别交x轴、y轴于点B,C,过点C作直线l的垂线交x轴于点A.若点A的坐标为(2,0)且AC=4,则在直线l上是否存在点P,使△PAB与△BOC相似?若存在,请求出该点坐标;若不存在,请说明理由. 如图,在矩形ABCD中,AB=7cm,BC=2$\sqrt{2}$cm,点P从点A出发沿AB以1cm/s的速度向点B移动,点P出发几秒后,点P、A的距离是点P、C的距离的2倍.
如图,在矩形ABCD中,AB=7cm,BC=2$\sqrt{2}$cm,点P从点A出发沿AB以1cm/s的速度向点B移动,点P出发几秒后,点P、A的距离是点P、C的距离的2倍.