题目内容
7.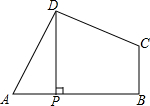 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是4,则DP的长是2.
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是4,则DP的长是2.
分析 作DE⊥BC,交BC延长线于E,如图,则四边形BEDP为矩形,再利用等角的余角相等得到∠ADP=∠CDE,则可利用“AAS”证明△ADP≌△CDE,得到DP=DE,S△ADP=S△CDE,所以四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,根据正方形的面积公式得到DP2=4,易得DP=2.
解答 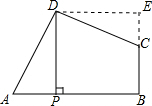 解:作DE⊥BC,交BC延长线于E,如图,
解:作DE⊥BC,交BC延长线于E,如图,
∵DP⊥AB,ABC=90°,
∴四边形BEDP为矩形,
∴∠PDE=90°,即∠CDE+∠PDC=90°,
∵∠ADC=90°,即∠ADP+∠PDC=90°,
∴∠ADP=∠CDE,
在△ADP和△CDE中
$\left\{\begin{array}{l}{∠APD=∠CED}\\{∠ADP=∠CDE}\\{AD=DC}\end{array}\right.$,
∴△ADP≌△CDE,
∴DP=DE,S△ADP=S△CDE,
∴四边形BEDP为正方形,S四边形ABCD=S矩形BEDP,
∴DP2=4,
∴DP=2.
故答案为2.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了正方形的性质和勾股定理.本题的关键的作辅助线构造两个全等的三角形.

练习册系列答案
相关题目
17.代数式15ax2-15a与10x2+20x+10的公因式是( )
| A. | 5(x+1) | B. | 5a(x+1) | C. | 5a(x-1) | D. | 5(x-1) |
2.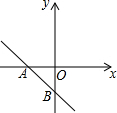 如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )
如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )
 如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )
如图,一次函数y=(m-1)x-3+m的图象分别于x轴、y轴的负半轴相交于点A、B,则m的取值范围是( )| A. | m>3 | B. | m<3 | C. | m>1 | D. | m<1 |
17.下列说法中,正确的是( )
| A. | 2是-4的算术平方根 | B. | -5是(-5)2的算术平方根 | ||
| C. | 16的平方根是±4 | D. | 27的立方根是±3 |