题目内容
12.不等式组$\left\{\begin{array}{l}{3x>-8}\\{x-4≤0}\end{array}\right.$的整数解是-2,-1,0,1,2,3,4.分析 分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出符合条件的x的整数解即可.
解答 解:$\left\{\begin{array}{l}{3x>-8①}\\{x-4≤0②}\end{array}\right.$
∵解不等式①,得:x>-$\frac{8}{3}$,
解不等式②,得:x≤4,
∴不等式组的解集为:-$\frac{8}{3}$<x≤4.
∴此不等式组的整数解为:-2,-1,0,1,2,3,4.
故答案为:-2,-1,0,1,2,3,4.
点评 本题考查的是求一元一此不等式组的整数解,求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
20.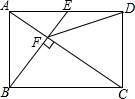 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
4.已知正整数中a、b、c,c=7且a<b<c,则以a、b、c为三边长的三角形共有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
2.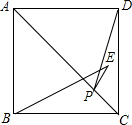 如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )
如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )
 如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )
如图,E是正方形ABCD内一点,BA=BE,P是对角线AC上的一点,若AC=$\sqrt{2}$,则PE+PD的最小值为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
 已知A(-1,2),B(-2,-1),将线段AB向右平移4个单位长度,再向下平移1个单位长度,得到线段A′B′.
已知A(-1,2),B(-2,-1),将线段AB向右平移4个单位长度,再向下平移1个单位长度,得到线段A′B′.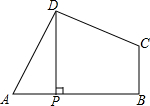 如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是4,则DP的长是2.
如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是4,则DP的长是2.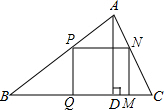 如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.
如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.若这个矩形的长是宽的2倍,求矩形的长和宽.