题目内容
19.(1)如图1,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.(2)如图2,已知Rt△ABC,∠C=90°.
①用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)
②若AB=10,CD=3,求△ABD的面积.
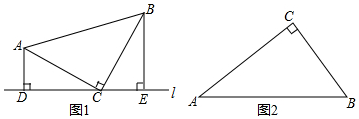
分析 (1)只要证明△ACD≌△CBE即可解决问题;
(2)①利用尺规作△ABC的角平分线即可;
②过点D作DE⊥AB于E.由DC⊥AC,DE⊥AB推出DE=DC=3,根据S△ABD=$\frac{1}{2}$•AB•DE计算即可;
解答 解:(1)∵∠ACB=90°,
∴∠ACD+∠BCE=90°
∵AD⊥l
∴∠ACD+∠CAD=90°
∴∠CAD=∠BCE.
∵BE⊥l,AD⊥l
∴∠ADC=∠BEC=90°
∵在△ACD和△CBE中,
$\left\{\begin{array}{l}{∠CAD=∠BCE\\;}\\{∠ADC=∠BEC=90°}\\{AC=BC}\end{array}\right.$
∴△ACD≌△CBE.
∴AD=CE,CD=BE.
∵DE=CD+CE
∴DE=AD+BE.
(2)①△ABC的角平分线AD如图所示.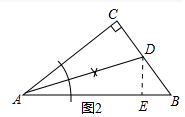
②解:过点D作DE⊥AB于E.
∵DC⊥AC,DE⊥AB
∴DE=DC=3,
∴S△ABD=$\frac{1}{2}$•AB•DE=$\frac{1}{2}$×10×3=15.
点评 本题考查基本作图、全等三角形的判定和性质、角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
10.等式$\sqrt{\frac{a}{2-a}}$=$\frac{\sqrt{a}}{\sqrt{2-a}}$成立的条件是( )
| A. | a≥0 | B. | 0≤a<2 | C. | a≠2 | D. | $\frac{a}{2-a}$≥0 |
14.如果一个三角形的两边长分别为5,12,则第三边的长可以是( )
| A. | 18 | B. | 13 | C. | 7 | D. | 5 |
11.若a<b,则下列各式一定成立的是( )
| A. | a-1<b-1 | B. | $\frac{a}{3}>\frac{b}{3}$ | C. | a2>b2 | D. | ac<bc |
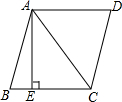 如图,在菱形ABCD中,AB=10,对角线AC=12,过点A作AE⊥BC,垂足为E,则AE的长为$\frac{48}{5}$.
如图,在菱形ABCD中,AB=10,对角线AC=12,过点A作AE⊥BC,垂足为E,则AE的长为$\frac{48}{5}$.