题目内容
9.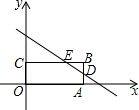 如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,点B在第一象限,直线y=$-\frac{2}{3}x+2$与边AB、BC分别交于点D、E,若点B的坐标为(m,1),则m的值可能是( )
如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,点B在第一象限,直线y=$-\frac{2}{3}x+2$与边AB、BC分别交于点D、E,若点B的坐标为(m,1),则m的值可能是( )| A. | -1 | B. | 1 | C. | 2 | D. | 4 |
分析 求出点E和直线y=-$\frac{2}{3}$x+2与x轴交点的坐标,即可判断m的范围,由此可以解决问题.
解答 解:∵B、E两点的纵坐标相同,B点的纵坐标为1,
∴点E的纵坐标为1,
∵点E在y=-$\frac{2}{3}$x+2上,
∴点E的坐标($\frac{3}{2}$,1),
∵直线y=-$\frac{2}{3}$x+2与x轴的交点为(3,0),
∴由图象可知点B的横坐标$\frac{3}{2}$<m<3,
∴m=2.
故选C.
点评 本题考查一次函数图象上的点的坐标特征,解题的关键是知道点的位置能确定点的坐标,是数形结合的好题目,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.圆锥的侧面展开图是( )
| A. | 扇形 | B. | 等腰三角形 | C. | 圆 | D. | 矩形 |
17. 如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
 如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )
如图,AB是⊙O的直径,∠BAD=70°,则∠ACD的大小为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
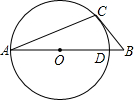 如图,AC是⊙O的弦,CB是⊙O的切线,C为切点,AB经过圆心与⊙O的交点为D,若∠B=50°,AD=10,则$\widehat{CD}$的长为$\frac{10}{9}$π.(结果保留π)
如图,AC是⊙O的弦,CB是⊙O的切线,C为切点,AB经过圆心与⊙O的交点为D,若∠B=50°,AD=10,则$\widehat{CD}$的长为$\frac{10}{9}$π.(结果保留π)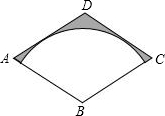 如图,菱形ABCD的对角线BD、AC的长分别为2,2$\sqrt{3}$,以点B为圆心的弧与AD、DC相切,则图中阴影部分的面积是2$\sqrt{3}$-π.
如图,菱形ABCD的对角线BD、AC的长分别为2,2$\sqrt{3}$,以点B为圆心的弧与AD、DC相切,则图中阴影部分的面积是2$\sqrt{3}$-π.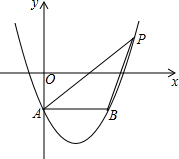 如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是2.
如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是2.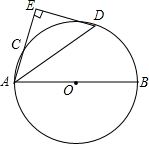 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.
如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.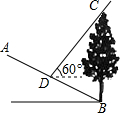 如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.
如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.