题目内容
2．若抛物线y=（x-2）2+（m+1）的顶点在第一象限，则m的取值范围为m＞-1．分析 直接利用顶点形式得出顶点坐标，结合第一象限点的特点列出不等式解答即可．
解答 解：∵抛物线y=（x-2）2+（m+1），
∴顶点坐标为（2，m+1），
∵顶点在第一象限，
∴m+1＞0，
∴m的取值范围为m＞-1．
故答案为：m＞-1．
点评 本题考查二次函数的性质，二次函数y=a（x-h）2+k的顶点坐标为（h，k），以及各个象限点的坐标特征．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
12．计算$\frac{{a}^{2}}{{b}^{3}}$$•\frac{2{b}^{2}}{3{a}^{2}}$的结果是（ ）
| A． | $\frac{2a}{3}$ | B． | $\frac{2b}{3}$ | C． | $\frac{2}{b}$ | D． | $\frac{2}{3b}$ |
17．
如图，AB是⊙O的直径，∠BAD=70°，则∠ACD的大小为（ ）
如图，AB是⊙O的直径，∠BAD=70°，则∠ACD的大小为（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 35° |
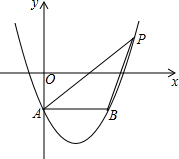如图，在平面直角坐标系中，抛物线y=x2-2x-1交y轴于点A，过点A作AB∥x轴交抛物线于点B，点P在抛物线上，连结PA、PB，若点P关于x轴的对称点恰好落在直线AB上，则△ABP的面积是2．