题目内容
2.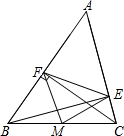 如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.
如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.(1)求证:ME=MF;
(2)若∠A=50°,求∠FME的度数.
分析 (1)根据直角三角形斜边上的中线等于斜边的一半得到ME=$\frac{1}{2}$BC,MF=$\frac{1}{2}$BC,得到答案;
(2)根据四点共圆的判定得到B、C、E、F四点共圆,根据圆周角定理得到答案.
解答 (1)证明:∵BE⊥AC,CF⊥AB,M为BC的中点,
∴ME=$\frac{1}{2}$BC,MF=$\frac{1}{2}$BC,
∴ME=MF;
(2)解:∵CF⊥AB,∠A=50°,
∴∠ACF=40°,
∵BE⊥AC,CF⊥AB,
∴B、C、E、F四点共圆,
∴∠FME=2∠ACF=80°.
点评 本题考查的是直角三角形的性质和四点共圆的知识,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
相关题目
 有一块长方体的水泥砖(如图所示),不借助于任何其他仪器,不经任何计算,利用笔和长度足够的刻度尺,测出长方体内最长的直线距离.
有一块长方体的水泥砖(如图所示),不借助于任何其他仪器,不经任何计算,利用笔和长度足够的刻度尺,测出长方体内最长的直线距离.