题目内容
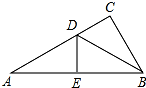如图，Rt△ABC中，∠C=90°，AB=5，BC=3，D、E分别是AC、AB上的点，且△ADE沿DE折叠后，点A恰好落在点B处，则CD+BD的长为考点：翻折变换（折叠问题）
专题：
分析：如图，证明BD=AD，这是解决该题的关键性结论；由勾股定理求出AC，即可解决问题．
解答：解：如图，由题意的：BD=AD，
∴CD+BD=CD+AD=AC；
∵∠C=90°，AB=5，BC=3，
∴AC2=AB2-BC2=16，
∴AC=4，
故答案为4．
∴CD+BD=CD+AD=AC；
∵∠C=90°，AB=5，BC=3，
∴AC2=AB2-BC2=16，
∴AC=4，
故答案为4．
点评：该题主要考查了翻折变换的性质及其应用问题；解题的关键是牢固掌握翻折变换的性质，这是灵活运用、解题的基础和关键．
练习册系列答案
名校课堂系列答案
相关题目
已知：如图，点A，B，C，D的坐标分别是（1，7），（1，1），（4，1），（6，1）．若以C，D，E（E在格点上）为顶点的三角形与△ABC相似，则满足条件的点E的坐标共有（ ）
如图，A，B是小河同侧的两个村庄，为解决吃水问题，两村合资在河边修一个水站．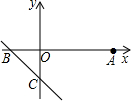
如图，已知A（2，0）、B（-1，0）、C（0，-1），在直线BC上是否存在一点P，使△ACP为等腰三角形？若存在，求点P的坐标；若不存在，说明理由．
如图，直线y=x-3与反比例函数y=
如图，是一个被分成6等份的扇形转盘，小明转了2次结果指针都停留在红色区域，小明第3次再转动指针停留在红色区域的概率是