题目内容
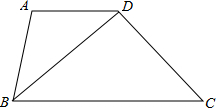如图，已知AD∥BC，BD是∠ABC的平分线，那么△ABD是等腰三角形吗？为什么？考点：等腰三角形的判定
专题：
分析：根据BD是∠ABC的平分线得到∠ABD=∠DBC，然后利用平行线性质得到∠ADB=∠DBC，从而∠ADB=∠ABD，进而证得△ABD是等腰三角形．
解答：解：△ABD是等腰三角形，
理由是：
∵BD是∠ABC的平分线
∴∠ABD=∠DBC
又∵AD∥BC
∴∠ADB=∠DBC（两直线平等，内错角相等）
∴∠ADB=∠ABD
∴△ABD是等腰三角形．
理由是：
∵BD是∠ABC的平分线
∴∠ABD=∠DBC
又∵AD∥BC
∴∠ADB=∠DBC（两直线平等，内错角相等）
∴∠ADB=∠ABD
∴△ABD是等腰三角形．
点评：本题利用了等腰三角形的判定及性质和平行线的性质；进行角的等量代换是正确解答本题的关键．
练习册系列答案
相关题目
禽流感病毒的形状一般为球形，直径大约为0.000000102m，该直径用科学记数法表示为（ ）
| A、1.02×10-7m |
| B、10.2×10-7m |
| C、1.02×10-6m |
| D、1.0×10-8m |
如图，已知第一象限内的点A在反比例函数y=| 2 |
| x |
| k |
| x |
| 2 |
A、-2
| ||
| B、4 | ||
| C、-4 | ||
D、2
|
如图，∠AOD=150°，∠AOB=40°，∠COD=70°，OM、ON分别是∠AOB、∠COD的平分线，求∠MON的度数．
如图所示，已知线段AB=12cm，点O是AB上一点，C为AO的中点，点D在线段OB上，且AO：OD：DB=3：2：1，求线段AC的长．
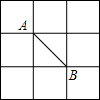如图，A，B是3×3的正方形网格中的两个格点，C也是网格中的一个格点，连接AC、BC，当△ABC为等腰三角形时，格点C的不同位置有（ ）| A、5个 | B、6个 | C、7个 | D、8个 |