��Ŀ����
18��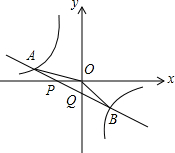 ��ͼ����ֱ֪��y=k1x+b��x�ᣬy���ཻ��P��Q���㣬��y=$\frac{{k}_{2}}{x}$��ͼ���ཻ��A��-2��m����B��1��n�����㣬����OA��OB���������н��ۣ���k1k2��0����m+$\frac{1}{2}$n=0����S��AOP=S��BOQ���ܲ���ʽk1x+b��$\frac{{k}_{2}}{x}$�Ľ⼯��x��-2��0��x��1��������ȷ�Ľ����ǣ�������
��ͼ����ֱ֪��y=k1x+b��x�ᣬy���ཻ��P��Q���㣬��y=$\frac{{k}_{2}}{x}$��ͼ���ཻ��A��-2��m����B��1��n�����㣬����OA��OB���������н��ۣ���k1k2��0����m+$\frac{1}{2}$n=0����S��AOP=S��BOQ���ܲ���ʽk1x+b��$\frac{{k}_{2}}{x}$�Ľ⼯��x��-2��0��x��1��������ȷ�Ľ����ǣ�������| A�� | �ڢۢ� | B�� | �٢ڢۢ� | C�� | �ۢ� | D�� | �ڢ� |
���� ����һ�κ����ͷ��������������ʵõ�k1k2��0���ʢٴ���A��-2��m����B��1��n������=$\frac{{k}_{2}}{x}$�еõ�m+$\frac{1}{2}$n=0���ʢ���ȷ����A��-2��m����B��1��n������y=k1x+b�õ�y=-mx+$\frac{3}{2}$m�����P��-$\frac{3}{2}$��0����Q��0��-m�������������ε������ʽ���ɵõ�S��AOP=S��BOQ���ʢ���ȷ������ͼ��õ�����ʽk1x+b��$\frac{{k}_{2}}{x}$�Ľ⼯��x��-2��0��x��1���ʢ���ȷ��
��� �⣺��ͼ��֪��k1��0��k2��0��
��k1k2��0���ʢٴ���
��A��-2��m����B��1��n������y=$\frac{{k}_{2}}{x}$�е�-2m=n��
��m+$\frac{1}{2}$n=0���ʢ���ȷ��
��A��-2��m����B��1��n������y=k1x+b��$\left\{\begin{array}{l}{m=-2{k}_{1}+b}\\{n={k}_{1}+b}\end{array}\right.$��
��$\left\{\begin{array}{l}{{k}_{1}=\frac{n-m}{3}}\\{b=\frac{2n+m}{3}}\end{array}\right.$��
��-2m=n��
��y=-mx-m��
����ֱ֪��y=k1x+b��x�ᡢy���ཻ��P��Q���㣬
��P��-1��0����Q��0��-m����
��OP=1��OQ=m��
��S��AOP=$\frac{1}{2}$m��S��BOQ=$\frac{1}{2}$m��
��S��AOP=S��BOQ���ʢ���ȷ��
��ͼ��֪����ʽk1x+b��$\frac{{k}_{2}}{x}$�Ľ⼯��x��-2��0��x��1���ʢ���ȷ��
��ѡA��
���� ���⿼���˷�����������һ�κ����Ľ��㣬����ֱ�ߵĽ������꣬����������ļ��㣬��ȷ�����������ǽ���Ĺؼ���

 ij����ʽ��Ľ⼯�������ϱ�ʾ��ͼ��ʾ�����������ʽ������ǣ�������
ij����ʽ��Ľ⼯�������ϱ�ʾ��ͼ��ʾ�����������ʽ������ǣ�������| A�� | $\left\{\begin{array}{l}x��4\\ x��-1\end{array}\right.$ | B�� | $\left\{\begin{array}{l}x��4\\ x��-1\end{array}\right.$ | C�� | $\left\{\begin{array}{l}x��4\\ x��-1\end{array}\right.$ | D�� | $\left\{\begin{array}{l}x��4\\ x��-1\end{array}\right.$ |
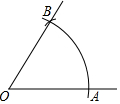 ��ͼ����OΪԲ�ģ����ⳤΪ�뾶������������OM���ڵ�A������AΪԲ�ģ�AO��Ϊ�뾶�������������ڵ�B��������OB������ж���AOBΪ�ȱ������ε�������������ȵ�������Ϊ�ȱ������Σ�
��ͼ����OΪԲ�ģ����ⳤΪ�뾶������������OM���ڵ�A������AΪԲ�ģ�AO��Ϊ�뾶�������������ڵ�B��������OB������ж���AOBΪ�ȱ������ε�������������ȵ�������Ϊ�ȱ������Σ�
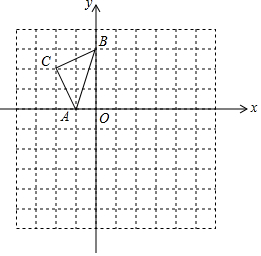 ��ͼ������֪��ƽ��ֱ������ϵ�У���ABC�Ķ��㶼������������ĸ���ϣ���A��B���������ֱ���A��-1��0����B��0��3����
��ͼ������֪��ƽ��ֱ������ϵ�У���ABC�Ķ��㶼������������ĸ���ϣ���A��B���������ֱ���A��-1��0����B��0��3����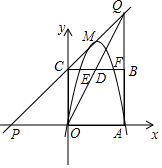 ��ͼ��������y=-x2+2mx��m��1����x���ڵ�O��A������ΪM����OAΪ�����Ϸ���������OABC��ֱ��CM��x���ڵ�P����ֱ��AB�ڵ�Q������OQ��ֱ��BC�ڵ�D��
��ͼ��������y=-x2+2mx��m��1����x���ڵ�O��A������ΪM����OAΪ�����Ϸ���������OABC��ֱ��CM��x���ڵ�P����ֱ��AB�ڵ�Q������OQ��ֱ��BC�ڵ�D��