题目内容
19.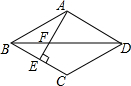 如图,BD是菱形ABCD的对角线,AE⊥BC于点E,交BD于点F,且E为BC的中点,则cos∠BFE的值是( )
如图,BD是菱形ABCD的对角线,AE⊥BC于点E,交BD于点F,且E为BC的中点,则cos∠BFE的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
分析 直接利用菱形的性质结合线段垂直平分线的性质得出AB=BC=AC,进而得出∠BFE=60°,即可得出答案.
解答 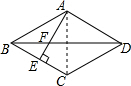 解:∵E为BC的中点,AE⊥BC,
解:∵E为BC的中点,AE⊥BC,
∴AB=AC,
∵四边形ABCD是菱形,
∴AB=BC,
∴AB=BC=AC,
∴△ABC是等边三角形,
∴∠ABC=60°,
∴∠ABD=∠CBD=30°,∠BAE=30°,
∴∠BFE=60°,
∴cos∠BFE=$\frac{1}{2}$.
故选:C.
点评 此题主要考查了菱形的性质以及等边三角形的判定与性质,得出△ABC是等边三角形是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若关于x的不等式组$\left\{\begin{array}{l}{x-a<1}\\{x≥1}\end{array}\right.$的整数解有3个,则a的取值范围是( )
| A. | 3<a≤4 | B. | 2<a≤3 | C. | 2≤a<3 | D. | 3≤a<4 |
7.若多项式m2-2m的值为2,则多项式2m2-4m-1的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.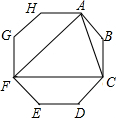 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )| A. | △ACF是等边三角形 | |
| B. | 连接BF,则BF分别平分∠AFC和∠ABC | |
| C. | 整个图形是轴对称图形,但不是中心对称图形 | |
| D. | 四边形AFGH与四边形CFED的面积相等 |
4. 如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=70°,则∠B的度数为( )
如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=70°,则∠B的度数为( )
 如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=70°,则∠B的度数为( )
如图,CF是△ABC的外角∠ACM的平分线,且CF∥AB,∠ACF=70°,则∠B的度数为( )| A. | 55° | B. | 60° | C. | 70° | D. | 75° |
11.关于数据:25,26,23,27,26,23,20.下列说法正确的是( )
| A. | 中位数是27 | B. | 众数是23和26 | C. | 极差是6 | D. | 平均数是24.5 |
 已知长方形的两条边长分别为4,6.建立适当的坐标系,使它的一个顶点的坐标为(-2,-3).画出示意图,然后写出其他各顶点的坐标.
已知长方形的两条边长分别为4,6.建立适当的坐标系,使它的一个顶点的坐标为(-2,-3).画出示意图,然后写出其他各顶点的坐标.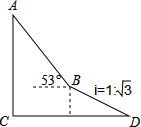 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).