题目内容
14.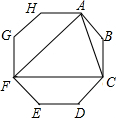 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )| A. | △ACF是等边三角形 | |
| B. | 连接BF,则BF分别平分∠AFC和∠ABC | |
| C. | 整个图形是轴对称图形,但不是中心对称图形 | |
| D. | 四边形AFGH与四边形CFED的面积相等 |
分析 由正八边形的性质得出A不正确,B、C、D正确,即可得出结论.
解答 解:∵八边形ABCDEFGH是正八边形,
∴AB=CB=AH=GH=GF=EF=DE=CD,AF=CF,∠AFC=90°-45°=45°,
∴∠FAC=∠FCA=(180°-45°)=67.5°,
∴△ACF不是等边三角形,选项A错误;
∵正八边形是轴对称图形,直线BF是对称轴,
∴连接BF,则BF分别平分∠AFC和∠ABC,
∴选项B、C正确;
∵四边形AFGH与四边形CFED的面积相等,
∴选项D正确;
故选:A.
点评 本题考查了正八边形的性质、等腰三角形的性质;熟记正八边形的性质是解决问题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
2.如果等边三角形的边长为8$\sqrt{2}$,那么等边三角形的中位线长为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
9.下列说法错误的是( )
| A. | 必然事件的概率为1 | |
| B. | 数据1、2、2、3的平均数是2 | |
| C. | 数据5、2、-3、0的方差为8.5 | |
| D. | 若某抽奖活动的中奖率为40%,则参加这种活动10次必有4次中奖 |
19.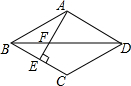 如图,BD是菱形ABCD的对角线,AE⊥BC于点E,交BD于点F,且E为BC的中点,则cos∠BFE的值是( )
如图,BD是菱形ABCD的对角线,AE⊥BC于点E,交BD于点F,且E为BC的中点,则cos∠BFE的值是( )
 如图,BD是菱形ABCD的对角线,AE⊥BC于点E,交BD于点F,且E为BC的中点,则cos∠BFE的值是( )
如图,BD是菱形ABCD的对角线,AE⊥BC于点E,交BD于点F,且E为BC的中点,则cos∠BFE的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
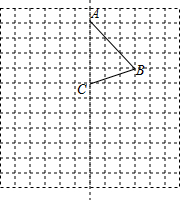 如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC. 如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.
如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.