题目内容
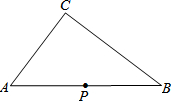如图，P是Rt△ABC斜边AB上一点（A、B两点除外），过点P作一直线，使截得的三角形与Rt△ABC相似，这样的直线可以作（ ）| A、1条 | B、2条 | C、3条 | D、4条 |
考点：相似三角形的判定
专题：
分析：根据相似三角形的判定方法进行求解．
解答：
解：过点P可作PE∥BC或PE′∥AC，可得相似三角形；
过点P还可作PE″⊥AB，可得：∠E″PA=∠C=90°，∠A=∠A，
故可得△APE∽△ACB；
所以共有3条．
故选：C．
解：过点P可作PE∥BC或PE′∥AC，可得相似三角形；过点P还可作PE″⊥AB，可得：∠E″PA=∠C=90°，∠A=∠A，
故可得△APE∽△ACB；
所以共有3条．
故选：C．
点评：此题考查了相似三角形的判定：
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
练习册系列答案
相关题目
平面直角坐标系内一点P（-3，2）关于原点对称的点的坐标是（ ）
| A、（2，-3） |
| B、（3，-2） |
| C、（-2，-3） |
| D、（2，3） |
下列化简，正确的是（ ）
| A、-[-（-10）]=-10 |
| B、-（-3）=-3 |
| C、-（+5）=5 |
| D、-[-（+8）]=-8 |
若分式
值为1，则x的值为（ ）
| |x|-2 |
| x-2 |
| A、x=2 | B、x≥0 |
| C、x≥2 | D、x≥0且x≠2 |
若抛物线y=x2-2x+c与y轴的交点为（0，-3），则下列说法不正确的是（ ）
| A、抛物线开口向上 |
| B、抛物线与x轴的交点为（-1，0），（3，0） |
| C、当x=1时，y的最大值为-4 |
| D、抛物线的对称轴是直线x=1 |
已知|4x+y-5|+|x-2y-4|=0，则x+y的值为（ ）
| A、1 | ||
B、
| ||
| C、0 | ||
D、-
|
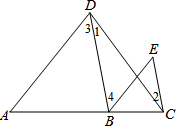按图填空，并注明理由．
如图，一次函数y=ax+b的图象与反比例函数y=