题目内容
6.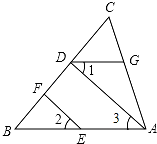 已知:∠CGD=∠CAB,∠1=∠2,AD⊥BC,求证:EF⊥BC.
已知:∠CGD=∠CAB,∠1=∠2,AD⊥BC,求证:EF⊥BC.
分析 首先利用平行线的判定定理和性质易得∠1=∠3,等量代换得∠2=∠3,再利用平行线的判定定理及垂直的定义易得结论.
解答 证明:∵∠CGD=∠CAB(已知),
∴DG∥AB(同位角相等,两直线平行),
∴∠1=∠3(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠2=∠3,
∴EF∥AD(内同位角相等,两直线平行),
∴∠EFB=∠ADB(两直线平行,同位角相等),
又∵AD⊥BC于点D(已知),
∴∠ADB=90°,
∴∠EFB=∠ADB=90°,
∴EF⊥CB.
点评 本题主要考查了平行线的判定定理及性质和垂直的定义,综合运用平行线的判定及性质定理是解答此题的关键.

练习册系列答案
相关题目
14.下列式子一定是二次根式的是( )
| A. | $\sqrt{-2}$ | B. | $\sqrt{0.03}$ | C. | $\sqrt{x}$ | D. | $\sqrt{-{x}^{2}-1}$ |
11.下列说法中正确的是:所有的( )都相似.
| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
18.下列各式无意义的是( )
| A. | -$\sqrt{3^2}$ | B. | $\sqrt{-{3^2}}$ | C. | $\sqrt{{{({-3})}^2}}$ | D. | $\sqrt{|{-3}|}$ |
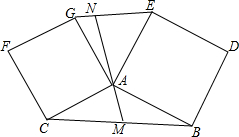 如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N.
如图,四边形ABDE和ACFG都是正方形,过A作直线l,交BC,GE于M、N. 如图,直线AB、CD交于点O,∠AOE=150°,且OE平分∠DOB,则∠AOC=60度.
如图,直线AB、CD交于点O,∠AOE=150°,且OE平分∠DOB,则∠AOC=60度. 如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40°.
如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120海里,乙巡逻艇每小时航行50海里,乙巡逻艇的航向为北偏西40°.