Question

5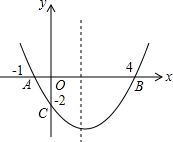．如图，在平面直角坐标系中，抛物线经过点A（-1，0），B（4，0），C（0，-2）．
（1）求此抛物线的解析式和对称轴．
（2）在此抛物线的对称轴上是否存在点P，使△PAC的周长最小？若存在，请求出点P的坐标；若不存在，说明理由．
（3）在抛物线上是否存在一点D，使△ABD是直角三角形？若存在，请求出点D的坐标；若不存在，请说明理由．

Answer 1

分析 （1）由抛物线过点C（0，-2），故设抛物线的解析式为y=ax²+bx-2，由点在抛物线的可列出关于a、b的二元一次方程组，解方程组即可得出抛物线的解析式，将解析式进行配方即可得出抛物线的对称轴；
（2）假设存在，由抛物线的对称性可知PA=PB，而当B、P、C三点共线时PB+PC最短，故找出直线BC的解析式，令x=$\frac{3}{2}$，求出y值，即可得出结论；
（3）假设存在，设出点D的坐标，结合抛物线的图象可知，△ABD是直角三角形边AB为斜边，由两点间的距离公式表示出各边的长度，结合勾股定理即可得出关于m的一元四次方程，解方程即可得出结论．

解答 解：（1）∵该抛物线过点C（0，-2），
∴可设该抛物线的解析式为y=ax²+bx-2，
将A（-1，0），B（4，0）代入，
得$\left\{\begin{array}{l}{0=a-b-2}\\{0=16a+4b-2}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{3}{2}}\end{array}\right.$．
∴此抛物线的解析式为y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2．
∵抛物线解析式为y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2=$\frac{1}{2}（x-\frac{3}{2}）^{2}$-$\frac{25}{8}$，
∴抛物线的对称轴为x=$\frac{3}{2}$．
（2）假设存在符合条件的点P，连接PB，如图所示．

由抛物线的对称性可知：PA=PB，
△PAC的周长C_△PAC=PA+PC+AC=PB+PC+AC，
∴当B、P、C三点共线时，PB+PC最小（三角形中两边之和大于第三边）．
设直线BC的解析式为y=kx+c，
将点B（4，0），点C（0，-2）代入，
得$\left\{\begin{array}{l}{0=4k+c}\\{-2=c}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{c=-2}\end{array}\right.$，
即直线BC的解析式为y=$\frac{1}{2}$x-2．
令x=$\frac{3}{2}$，则有y=$\frac{1}{2}×\frac{3}{2}$-2=-$\frac{5}{4}$，
即点P的坐标为（$\frac{3}{2}$，-$\frac{5}{4}$）．
故在此抛物线的对称轴上存在点P，使△PAC的周长最小，点P的坐标为（$\frac{3}{2}$，-$\frac{5}{4}$）．
（3）假设存在，设点D的坐标为（m，$\frac{1}{2}{m}^{2}$-$\frac{3}{2}$m-2），
∵点A（-1，0），点B（4，0），
∴由两点间的距离公式可知：AB=4-（-1）=5，AD=$\sqrt{（m+1）^{2}+（\frac{1}{2}{m}^{2}-\frac{3}{2}m-2）^{2}}$，BD=$\sqrt{（m-4）^{2}+（\frac{1}{2}{m}^{2}-\frac{3}{2}m-2）^{2}}$．
∵△ABD是直角三角形，且结合二次函数图象可知AB只能为斜边，
∴AD²+BD²=AB²，即$（m+1）^{2}+（m-4）^{2}+2（\frac{1}{2}{m}^{2}-\frac{3}{2}m-2）^{2}$=25，
整理得：m（m+1）（m-3）（m-4）=0，
解得：m₁=0，m₂=-1（舍去），m₃=3，m₄=4（舍去），
此时点D的坐标为（0，-2）或（3，-2）．
故在抛物线上存在一点D，使△ABD是直角三角形，点D的坐标为（0，-2）或（3，-2）．

点评 本题考查了待定系数法求函数解析式、抛物线的对称性、两点间的距离公式以及勾股定理等知识，解题的关键：（1）利用待定系数法求函数解析式；（2）由三角形中两边之和大于第三边寻找点P的位置；（3）结合两点间的距离公式和勾股定理列出方程．本题属于中档题，难度不大，（1）（2）较简单；（3）用到了分解因式解一元四次方程，稍显繁琐．