题目内容
4.某险种的基本保险费为a(单位:元),继续购买该险种的投保人称为续保人,保险公司规定:续保人本年度的保险费与其上年度出现次数有关,具体规定如下:| 上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 本年度保险费(元) | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
| 出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
| 频数 | 30 | 30 | m | 15 | 10 | 5 |
(Ⅱ)在这100名续保人中随机抽取1名续保人,求其本年度保险费不高于基本保险费的概率;
(Ⅲ)请估计续保人本年度保险费的平均值.(结果用含a的代数式表示)
分析 (1)根据各频数之和为100进行计算,即可得到m的值;
(2)根据本年度保险费不高于基本保险费的频数除以100,即可得到本年度保险费不高于基本保险费的概率;
(3)根据人数与保费乘积的和除以总续保人数,可得本年度的平均保费估计值.
解答 解:(1)由题可得,m=100-30-30-15-10-5=10,
故答案为:10;
(2)本年度保险费不高于基本保险费的频数为:30+30=60,
∴P(本年度保险费不高于基本保险费)=$\frac{60}{100}$=$\frac{3}{5}$;
(3)续保人本年度保险费的平均值=(0.85a×30+a×30+1.25a×10+1.5a×15+1.75a×10+2a×5)÷100=1.18a元.
点评 本题主要考查了概率公式以及频数分布表的应用,解题时注意:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.

练习册系列答案
相关题目
14.若分式$\frac{{x}^{2}+2x}{x}$的值为0,则x的值为( )
| A. | 2或0 | B. | 2 | C. | -2或0 | D. | -2 |
 如图,某计算机中有
如图,某计算机中有 、
、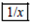 、
、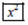 三个按键,以下是这三个按键的功能.
三个按键,以下是这三个按键的功能.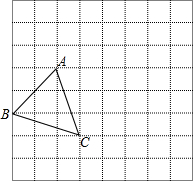 已知:如图在8×8的正方形网格中,每个小正方形的边长为1个单位长度,△ABC的每个顶点都在格点(每个小正方形的顶点)上,把△ABC向右平移4个单位,再向上平移1个单位得△A1B1C1;
已知:如图在8×8的正方形网格中,每个小正方形的边长为1个单位长度,△ABC的每个顶点都在格点(每个小正方形的顶点)上,把△ABC向右平移4个单位,再向上平移1个单位得△A1B1C1;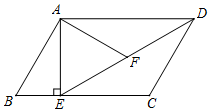 如图,平行四边形ABCD中,过点A作AE⊥BC于E,连接DE,F为DE中点,且∠BAE=∠DEC,∠B=60°.
如图,平行四边形ABCD中,过点A作AE⊥BC于E,连接DE,F为DE中点,且∠BAE=∠DEC,∠B=60°.