题目内容
13.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20都是“神秘数”(1)28和2014这两个数是“神秘数”吗?为什么?
(2)设两个连续偶数为2k和2k+2(k取非负整数),由这两个连续偶数构造的“神秘数”是4的倍数吗?为什么?
(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?
分析 (1)利用神秘数的定义判断即可;
(2)根据题意表示出两个连续偶数的平方差,利用平方差公式化简即可做出判断;
(3)利用神秘数得定义判断可得结果.
解答 解:(1)∵28=82-62,
∴28是神秘数;
2014不是神秘数,神秘数必须是4的倍数;
(2)两个连续偶数构造的“神秘数”是4的倍数,
∵(2k+2)2-(2k)2=8k+4=4(2k+1),
∴神秘数是4的倍数;
(3)不是,根据定义得到神秘数是两个连续偶数的平方差.
点评 此题考查了平方差公式,弄清题中“神秘数”的定义是解本题的关键.

练习册系列答案
相关题目
3.下列运算正确的是( )
| A. | a2×a3=a6 | B. | 2$\sqrt{3}×\sqrt{3}÷\sqrt{3}=2\sqrt{3}$ | C. | x2-5x+6=(x-6)(x+1) | D. | a2+a3=a5 |
18.三角形的角平分线是( )
| A. | 直线 | B. | 线段 | C. | 射线 | D. | 无法确定 |
 如图,AB、CD相交于点E,AD=AB,CB=CE,F、G、H分别是边DE、BE、AC的中点.
如图,AB、CD相交于点E,AD=AB,CB=CE,F、G、H分别是边DE、BE、AC的中点.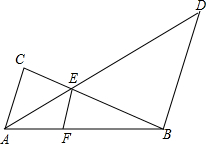 如图,AC∥BD,AD和BC相交于点E,EF∥AC交AB于点F,且AE=p,BD=q,EF=r.
如图,AC∥BD,AD和BC相交于点E,EF∥AC交AB于点F,且AE=p,BD=q,EF=r.