题目内容
8. 如图,AB、CD相交于点E,AD=AB,CB=CE,F、G、H分别是边DE、BE、AC的中点.
如图,AB、CD相交于点E,AD=AB,CB=CE,F、G、H分别是边DE、BE、AC的中点.(1)猜想:AF与DE、CG与AB有怎样的位置关系?为什么?
(2)猜想;FH与GH的大小有什么关系?请说明理由.
分析 (1)根据等腰三角形三线合一的性质即可证得AF⊥DE,CG⊥AB;
(2)根据直角三角形斜边中线的性质即可证得FH=$\frac{1}{2}$AC,GH=$\frac{1}{2}$AC,从而证得FH=GH.
解答 解:(1)AF⊥DE,CG⊥AB,
理由:∵AD=AE,F是边DE的中点.
∴AF⊥DE,
同理:CG⊥AB;
(2)FH=GH,
理由:∵AF⊥DE,
∴△AFC是直角三角形,
∵H是AC的中点.
∴FH=$\frac{1}{2}$AC,
同理:GH=$\frac{1}{2}$AC,
∴FH=GH.
点评 本题考查了等腰三角形的性质和直角三角形斜边中线的性质,熟练掌握三角形的性质是解题的关键.

练习册系列答案
相关题目

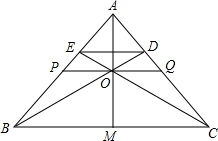 如图,已知:△ABC中,M为BC边的中点,O为AM上一点,BO的延长线交AC于点D,CO延长线交AB于点E,PQ∥BC,且PQ过点O与AB、AC分别交于P和点Q,求证:
如图,已知:△ABC中,M为BC边的中点,O为AM上一点,BO的延长线交AC于点D,CO延长线交AB于点E,PQ∥BC,且PQ过点O与AB、AC分别交于P和点Q,求证: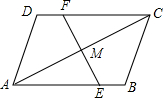 如图,在平行四边形ABCD中,E、F分别为边AB、DC上的点,连接EF交AC于点M.,且EF平分AC.
如图,在平行四边形ABCD中,E、F分别为边AB、DC上的点,连接EF交AC于点M.,且EF平分AC.