题目内容
4.若关于x的方程2x2-mx+1=0的两根正好是某直角三角形两锐角的正弦,则m的值为2$\sqrt{2}$.分析 设方程2x2-mx+1=0的两根分别为x1、x2,根据根与系数的关系即可得出x1+x2=$\frac{m}{2}$、x1•x2=$\frac{1}{2}$,再根据x1、x2是某直角三角形两锐角的正弦,即可得出关于m的一元二次方程且m为正值,解之即可得出结论.
解答 解:设方程2x2-mx+1=0的两根分别为x1、x2,
则有:x1+x2=$\frac{m}{2}$,x1•x2=$\frac{1}{2}$.
∵x1、x2是某直角三角形两锐角的正弦,
∴x1>0,x2>0,x1+x2=$\frac{m}{2}$>0,
∴${{x}_{1}}^{2}$+${{x}_{2}}^{2}$=$({x}_{1}+{x}_{2})^{2}$-2x1•x2=$\frac{{m}^{2}}{4}$-1=1,
解得:m=2$\sqrt{2}$或m=-2$\sqrt{2}$(舍去).
故答案为:2$\sqrt{2}$.
点评 本题考查了根与系数的关系、解直角三角形以及解一元二次方程,根据方程两根为某直角三角形两锐角的正弦列出关于m的一元二次方程是解题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
12.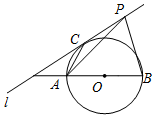 如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
 如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )| A. | 6 | B. | $6\sqrt{3}$ | C. | 9 | D. | $3\sqrt{3}$ |




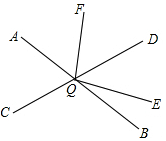 如图,直线AB、CD相交于点O,∠DOE:∠DOB=4:5,OF平分∠AOD,∠AOC=∠AOF-15°,则∠EOF的度数为105°.
如图,直线AB、CD相交于点O,∠DOE:∠DOB=4:5,OF平分∠AOD,∠AOC=∠AOF-15°,则∠EOF的度数为105°. 如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠EOC=62°,求∠AOB的度数.
如图,已知直线AD与BE相交于点O,∠DOE与∠COE互余,∠EOC=62°,求∠AOB的度数.