题目内容
12.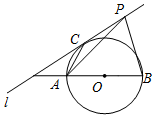 如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )
如图,直线l与以线段AB为直径的圆相切于点C,AB=6,AC=3,点P是直线l上一个动点.当∠APB的度数最大时,线段BP的长度为( )| A. | 6 | B. | $6\sqrt{3}$ | C. | 9 | D. | $3\sqrt{3}$ |
分析 连接BC,由题意可知当P和C重合时,∠APB的度数最大,根据勾股定理求出BC即可.
解答 解:连接BC,
∵直线l与以线段AB为直径的圆相切于点C,
∴∠ACB=90°,
当∠APB的度数最大时,
则P和C重合,
∴∠APB=90°,
∵AB=6,AC=3,
由勾股定理得:BP=BC=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
故选D.
点评 本题考查了切线的性质,圆周角定理以及勾股定理的有关知识,解题的关键是由题意可知当P和C重合时,∠APB的度数最大为90°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.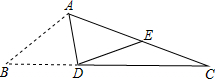 如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
 如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )
如图,AD是△ABC的角平分线,∠C=20°,AB+BD=AC,将△ABD沿AD所在直线翻折,点B在AC边上的落点记为点E,那么∠AED等于( )| A. | 80° | B. | 60° | C. | 40° | D. | 30° |
7.下列命题中是真命题的是( )
| A. | 确定性事件发生的概率为1 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 正n边形都是轴对称图形,并且有n条对称轴 | |
| D. | 两边及其一边的对角对应相等的两个三角形全等 |
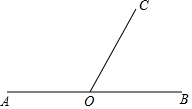 如图,∠AOC=2∠BOC,过点O作OD⊥OC,则∠BOD的度数为150°或30°.
如图,∠AOC=2∠BOC,过点O作OD⊥OC,则∠BOD的度数为150°或30°. 如图,在△ABC中,∠C=90°,点D在BC上,AD=BD=5,cos∠ADC=$\frac{3}{4}$.
如图,在△ABC中,∠C=90°,点D在BC上,AD=BD=5,cos∠ADC=$\frac{3}{4}$. 如图,若△AOB≌△COD,∠B=30°,∠AOC=52°,则∠CEO的度数为82°.
如图,若△AOB≌△COD,∠B=30°,∠AOC=52°,则∠CEO的度数为82°.