题目内容
1.(1)用配方法解方程:3x2-6x-1=0(2)求不等式2(1-3x)≥2x-30的正整数解.
分析 (1)先把方程两边都除以3,使二次项的系数为1,然后再配上一次项系数一半的平方,利用配方法解方程即可;
(2)首先利用不等式的基本性质解不等式,再从不等式的解集中找出适合条件的正整数即可.
解答 解:(1)把方程x2-2x-$\frac{1}{3}$=0的常数项移到等号的右边,得:x2-2x=$\frac{1}{3}$,
方程两边同时加上一次项系数一半的平方,得:x2-2x+1=$\frac{1}{3}$+1
配方得(x-1)2=$\frac{4}{3}$
开方得x-1=$\frac{2\sqrt{3}}{3}$
移项得x=±$\frac{2\sqrt{3}}{3}$+1,
即x1=$\frac{2\sqrt{3}+3}{3}$,x2=$\frac{-2\sqrt{3}+3}{3}$.
(2)∵2(1-3x)≥2x-30,
∴2-6x-2x≥-30,
解得x≤4,
∴不等式的正整数解为1,2,3,4.
点评 (1)本题考查了用配方法解一元二次方程,配方法的一般步骤:①把常数项移到等号的右边;②把二次项的系数化为1;③等式两边同时加上一次项系数一半的平方.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(2)本题考查了一元一次不等式的整数解,正确解不等式,求出解集是解答本题的关键.解不等式应根据不等式的基本性质.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
11.如图1,抛物线y=-x2+bx+c的顶点为P,与x轴交于A,B两点.若A,B两点间的距离为m,n是m的函数,且表示n与m的函数关系的图象大致如图2所示,则n可能为( )


| A. | PA+AB | B. | PA-AB | C. | $\frac{AB}{PA}$ | D. | $\frac{PA}{AB}$ |
11. 如图,已知直线AB是线段CD的垂直平分线,下列说法正确的是( )
如图,已知直线AB是线段CD的垂直平分线,下列说法正确的是( )
 如图,已知直线AB是线段CD的垂直平分线,下列说法正确的是( )
如图,已知直线AB是线段CD的垂直平分线,下列说法正确的是( )| A. | AC=BC | B. | AD=BD | C. | BC=BD | D. | AB=CD |
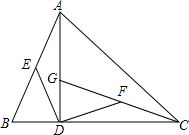 已知:如图,在△ABC中,∠ACB=45°,AD是边BC上的高,G是AD上一点,联结CG,点E、F分别是AB、CG的中点,且DE=DF.求证:△ABD≌△CGD.
已知:如图,在△ABC中,∠ACB=45°,AD是边BC上的高,G是AD上一点,联结CG,点E、F分别是AB、CG的中点,且DE=DF.求证:△ABD≌△CGD.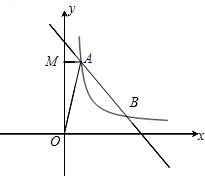 如图,一次函数y=mx+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,
如图,一次函数y=mx+5的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M,