题目内容
11.如图1,抛物线y=-x2+bx+c的顶点为P,与x轴交于A,B两点.若A,B两点间的距离为m,n是m的函数,且表示n与m的函数关系的图象大致如图2所示,则n可能为( )
| A. | PA+AB | B. | PA-AB | C. | $\frac{AB}{PA}$ | D. | $\frac{PA}{AB}$ |
分析 首先用m表示出PA,写出PA+AB,PA-AB,$\frac{AB}{PA}$,$\frac{PA}{AB}$,根据图象2即可判断.
解答 解;设A(x1,0),B(x2,0),则m=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{b}^{2}+4c}$,
∵顶点P($\frac{b}{2}$,$\frac{{b}^{2}+4c}{4}$)
∴顶点P纵坐标为$\frac{{m}^{2}}{4}$,
∴PA=$\sqrt{(\frac{m}{2})^{2}+(\frac{{m}^{2}}{4})^{2}}$=$\frac{m}{4}$•$\sqrt{{m}^{2}+4}$,
∵PA+AB=$\frac{m}{4}$•$\sqrt{{m}^{2}+4}$+m,
PA-AB=$\frac{m}{4}$•$\sqrt{{m}^{2}+4}$-m,
$\frac{AB}{PA}$=$\frac{4}{\sqrt{{m}^{2}+4}}$,
$\frac{PA}{AB}$=$\frac{\sqrt{{m}^{2}+4}}{4}$.
由图2可知,n可能是$\frac{AB}{PA}$.
故选C.
点评 本题考查抛物线与x轴交点,根与系数关系等知识,解题的关键是学会用参数解决问题,属于中考选择题中的压轴题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
6.星期日上午小明骑车去姥姥家吃午饭.已知从小明家去姥姥家的路是上坡路,吃过午饭后,下午按原路返回,设小明从家出发后所用的时间为x(小时),骑车所走的路程为y(千米),则y与x的函数图象大致是( )
| A. | 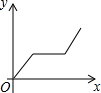 | B. | 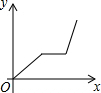 | C. | 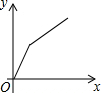 | D. | 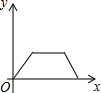 |
16.直线y=kx-1与y=x-1平行,则y=kx-1的图象经过的象限是( )
| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
20.在2,0,-3,-5中,最小的数是( )
| A. | 2 | B. | -5 | C. | -3 | D. | 0 |
